题目内容
如图,过抛物线 的对称轴上任一点
的对称轴上任一点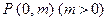 作直线与抛物线交于
作直线与抛物线交于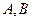 两点,点
两点,点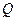 是点
是点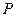 关于原点的对称点.
关于原点的对称点.
(1) 设点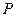 分有向线段
分有向线段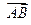 所成的比为
所成的比为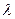 ,证明:
,证明:
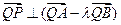 ;
;
(2) 设直线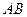 的方程是
的方程是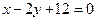 ,过
,过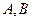 两点的圆
两点的圆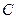 与抛物线在点
与抛物线在点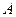 处有共同的切线,求圆
处有共同的切线,求圆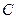 的方程.
的方程.
 的对称轴上任一点
的对称轴上任一点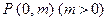 作直线与抛物线交于
作直线与抛物线交于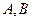 两点,点
两点,点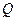 是点
是点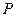 关于原点的对称点.
关于原点的对称点.(1) 设点
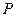 分有向线段
分有向线段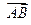 所成的比为
所成的比为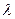 ,证明:
,证明:
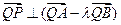 ;
;(2) 设直线
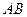 的方程是
的方程是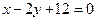 ,过
,过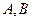 两点的圆
两点的圆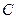 与抛物线在点
与抛物线在点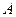 处有共同的切线,求圆
处有共同的切线,求圆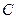 的方程.
的方程.(1)证明见解析(2)圆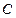 的方程是
的方程是 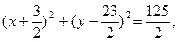 (或
(或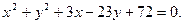 )
)
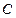 的方程是
的方程是 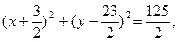 (或
(或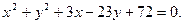 )
)(1) 依题意,可设直线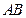 的方程为
的方程为 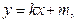 代入抛物线方程
代入抛物线方程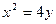 得
得
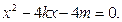 ①
①
设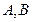 两点的坐标分别是
两点的坐标分别是 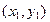 、
、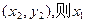 、
、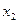 是方程①的两根.
是方程①的两根.
所以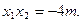
由点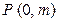 分有向线段
分有向线段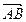 所成的比为
所成的比为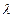 ,得
,得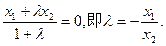
又点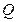 与点
与点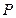 关于原点对称,故点
关于原点对称,故点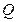 的坐标是
的坐标是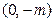 ,从而
,从而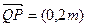 .
.
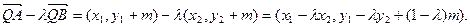
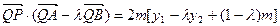
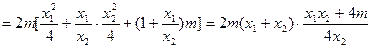
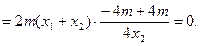 所以
所以 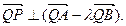
(2) 由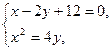 得点
得点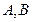 的坐标分别是(6,9)、(-4,4),
的坐标分别是(6,9)、(-4,4),
由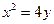 得
得 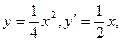
所以抛物线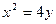 在点
在点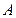 处切线的斜率为
处切线的斜率为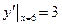 ,
,
设圆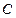 的圆心为
的圆心为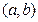 , 方程是
, 方程是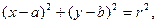
则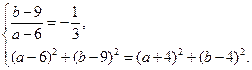 解得
解得 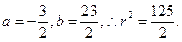
则圆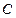 的方程是
的方程是 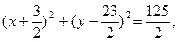 (或
(或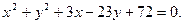 )
)
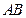 的方程为
的方程为 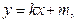 代入抛物线方程
代入抛物线方程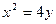 得
得 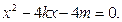 ①
①设
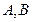 两点的坐标分别是
两点的坐标分别是 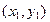 、
、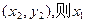 、
、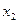 是方程①的两根.
是方程①的两根.所以
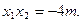
由点
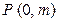 分有向线段
分有向线段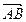 所成的比为
所成的比为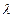 ,得
,得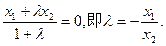
又点
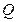 与点
与点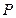 关于原点对称,故点
关于原点对称,故点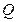 的坐标是
的坐标是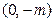 ,从而
,从而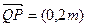 .
. 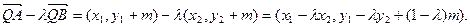
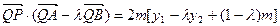
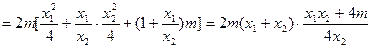
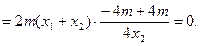 所以
所以 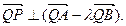
(2) 由
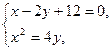 得点
得点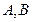 的坐标分别是(6,9)、(-4,4),
的坐标分别是(6,9)、(-4,4), 由
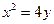 得
得 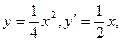
所以抛物线
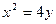 在点
在点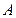 处切线的斜率为
处切线的斜率为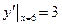 ,
, 设圆
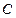 的圆心为
的圆心为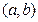 , 方程是
, 方程是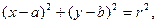
则
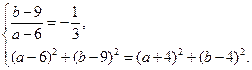 解得
解得 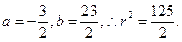
则圆
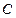 的方程是
的方程是 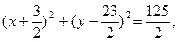 (或
(或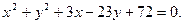 )
)
练习册系列答案
相关题目
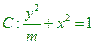 ;(1)由曲线C上任一点E向X轴作垂线,垂足为F,
;(1)由曲线C上任一点E向X轴作垂线,垂足为F,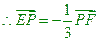 。问:点P的轨迹可能是圆吗?请说明理由;(2)如果直线L的斜率为
。问:点P的轨迹可能是圆吗?请说明理由;(2)如果直线L的斜率为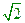 ,且过点
,且过点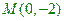 ,直线L交曲线C于A,B两点,又
,直线L交曲线C于A,B两点,又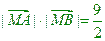 ,求曲线C的方程。
,求曲线C的方程。 
 轴上,它的一个顶点恰好是抛物线
轴上,它的一个顶点恰好是抛物线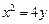 的焦点,离心率
的焦点,离心率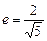 ,过椭圆的右焦点
,过椭圆的右焦点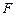 作与坐标轴不垂直的直线
作与坐标轴不垂直的直线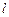 交椭圆于
交椭圆于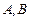 两点.
两点.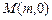 是线段
是线段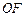 上的一个动点,且
上的一个动点,且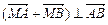 ,求
,求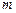 的取值范围;
的取值范围;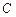 是点
是点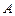 关于
关于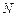 ,使得
,使得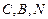 三点共线?若存在,求出定点
三点共线?若存在,求出定点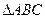 的两个顶点分别
的两个顶点分别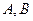 的坐标为
的坐标为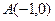 ,
,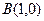 ,平面内两点
,平面内两点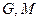 同时满足下列条件:
同时满足下列条件: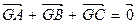 ;②
;②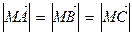 ;③
;③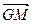 ∥
∥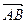
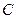 的轨迹方程;
的轨迹方程;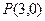 的直线
的直线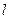 与(1)中轨迹交于
与(1)中轨迹交于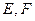 两点,求
两点,求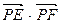 的取值范围
的取值范围

 的最值
的最值 平面上,
平面上,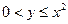 ,
,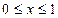 所围成图形的面积为
所围成图形的面积为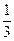 ,则集合
,则集合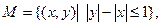
 的交集
的交集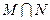 所表示的图形面积为
所表示的图形面积为  (C)
(C)  (B)
(B) 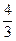 . ( )
. ( )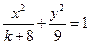 的离心率为
的离心率为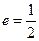 ,求
,求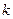 的值.
的值.