题目内容
15.已知h(x)=2sin(x+$\frac{π}{3}$)(0≤x≤$\frac{π}{2}$),则使得关于方程h(x)-t=0在[0,$\frac{π}{2}$]内恒有两个不相等实数解的实数t的取值范围为:[$\sqrt{3}$,2).分析 根据三角函数的图象和性质,将方程转化为两个函数的相交问题,即可得到结论.
解答 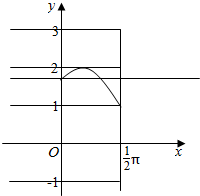 解:由h(x)-t=0的h(x)=t,
解:由h(x)-t=0的h(x)=t,
即2sin(x+$\frac{π}{3}$)=t,
设f(x)=2sin(x+$\frac{π}{3}$),
∵x∈[0,$\frac{π}{2}$],
∴x+$\frac{π}{3}$∈[$\frac{π}{3}$,$\frac{5π}{6}$],
作出函数f(x)=2sin(x+$\frac{π}{3}$),在0≤x≤$\frac{π}{2}$上的图象如图:
f(0)=2sin$\frac{π}{3}$=$2×\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
若2sin(x+$\frac{π}{3}$)=t,在[0,$\frac{π}{2}$]内恒有两个不相等实数解,
则$\sqrt{3}$≤t<2,
故实数t的取值范围为[$\sqrt{3}$,2).
故答案为:[$\sqrt{3}$,2)
点评 本题主要考查三角函数的图象和性质,利用数形结合是解决本题的关键.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
5.函数f(x)=x3-3x2+7的极值是( )
| A. | 有极大值无极小值 | B. | 有极小值无极大值 | ||
| C. | 无极大值也无极小值 | D. | 既有极大值也无极小值 |
6.“x>0”是“$\frac{1}{x}$>2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
10.设△ABC的内角A,B,C所对边的长分别为a,b,c,若a是b,c的等差中项,3sinA=5sinB,则角C=( )
| A. | 60° | B. | 120° | C. | 135° | D. | 150° |
7.已知a>0,如果P=$\sqrt{a}$+$\sqrt{a+3}$,Q=$\sqrt{a+1}$+$\sqrt{a+2}$,则( )
| A. | P>Q | B. | P<Q | ||
| C. | P=Q | D. | P与Q无法比较大小 |