题目内容

5．函数f（x）=x3-3x2+7的极值是（　　）
A．有极大值无极小值B．有极小值无极大值
C．无极大值也无极小值D．既有极大值也无极小值

分析 由已知得f′（x）=3x2-6x，由f′（x）=0，得x=0或x=2，由此能求出函数既有极大值又有极小值．

解答 解：f′（x）=3x2-6x，
由f′（x）=0，得x=0或x=2，
当f′（x）＞0时，解得x＜0或x＞2，函数单调递增，
当f′（x）＜0时，解得0＜x＜2，函数单调递减，
∴当x=0时，函数有极大值，当x=2是函数有极小值，
∴函数f（x）=x3-3x2+7既有极大值又有极小值．
故选：D

点评 本题考查函数的单调区间的求法，考查实数的极值的求法，解题时要认真审题，注意导数性质和分类讨论思想的合理运用，属于基础题．

练习册系列答案
相关题目
15．已知函数y=x2与y=kx（k＞0）的图象所围成的封闭区域的面积为$\frac{9}{2}$，则k=3．
16．如图所示的程序框图的运行结果是（　　）
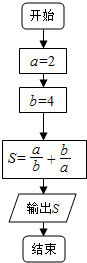
A．2B．2.5C．3.5D．4
13．已知函数y=f（x）的图象在点M（-1，f（-1））处的切线的方程是y=2x-1，则f（-1）+f′（-1）=-1．
20．下列说法正确的是（　　）
A．对于相关系数r来说，|r|≤1，|r|越接近0，相关程度越大；|r|越接近1，相关程度越小
B．对于相关系数r来说，|r|≥1，|r|越接近1，相关程度越大；|r|越大，相关程度越小
C．对于相关系数r来说，|r|≤1，|r|越接近1，相关程度越大；|r|越接近0，相关程度越小
D．对于相关系数r来说，|r|≥1，|r|越接近1，相关程度越小；|r|越大，相关程度越大
10．若关于x的不等式|x-2|+|x+4|＜a的解集是空集，则实数a的取值范围是（-∞，6]．
17．在中俄两国联合军事反恐演习中，为了准确分析形势，军方在底面上选择相距$\sqrt{3}$km的C，D两点，以测出对方两目标A和B的距离，经测量的：∠ACB=75°，∠BCD=45°，∠ADC=30°，∠ADB=45°，试求出A，B之间的距离．
14．计算i2-3=（　　）
A．2B．-4C．-1D．-2
15．已知h（x）=2sin（x+$\frac{π}{3}$）（0≤x≤$\frac{π}{2}$），则使得关于方程h（x）-t=0在[0，$\frac{π}{2}$]内恒有两个不相等实数解的实数t的取值范围为：[$\sqrt{3}$，2）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网