题目内容
12.已知直线y=-x+1与圆C:x2+y2-4x+3=0相较于A,B两点,则|AB|的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
分析 由条件可得圆心坐标和半径,利用点到直线的距离公式求出弦心距,再利用弦长公式求得弦长|AB|的值.
解答 解:由圆C:x2+y2-4x+3=0,可得圆心为C(2,0),半径r=1,
求得弦心距d=$\frac{|2+0-1|}{\sqrt{2}}$=$\frac{1}{\sqrt{2}}$,故弦长|AB|=2$\sqrt{1-\frac{1}{2}}$=$\sqrt{2}$.
故选:C.
点评 本题主要考查直线和圆相交的性质,点到直线的距离公式,弦长公式的应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.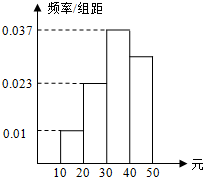 学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n的样本,其频率分布直方图如右图所示,其中支出在[40,50)元的同学有39人,则n的值为( )
学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n的样本,其频率分布直方图如右图所示,其中支出在[40,50)元的同学有39人,则n的值为( )
 学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n的样本,其频率分布直方图如右图所示,其中支出在[40,50)元的同学有39人,则n的值为( )
学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n的样本,其频率分布直方图如右图所示,其中支出在[40,50)元的同学有39人,则n的值为( )| A. | 100 | B. | 120 | C. | 130 | D. | 390 |
3.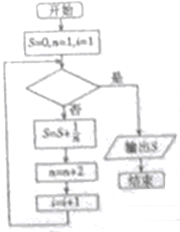 如图给出的是计算$\frac{1}{1}$+$\frac{1}{3}$+$\frac{1}{5}$+$\frac{1}{7}$+…+$\frac{1}{2015}$的一个程序框图,其中判断框内应填入的条件是( )
如图给出的是计算$\frac{1}{1}$+$\frac{1}{3}$+$\frac{1}{5}$+$\frac{1}{7}$+…+$\frac{1}{2015}$的一个程序框图,其中判断框内应填入的条件是( )
 如图给出的是计算$\frac{1}{1}$+$\frac{1}{3}$+$\frac{1}{5}$+$\frac{1}{7}$+…+$\frac{1}{2015}$的一个程序框图,其中判断框内应填入的条件是( )
如图给出的是计算$\frac{1}{1}$+$\frac{1}{3}$+$\frac{1}{5}$+$\frac{1}{7}$+…+$\frac{1}{2015}$的一个程序框图,其中判断框内应填入的条件是( )| A. | i<1008 | B. | i>1008 | C. | i<1009 | D. | i>1009 |
20.设向量$\overrightarrow{a}$=(cos2x,sinx),$\overrightarrow{b}$=(1,2cosx),将函数f(x)=$\overrightarrow{a}$,$\overrightarrow{b}$的图象向左平移φ(0<φ<π)个单位,得到函数g(x)的图象,若g(x)为奇函数,则φ的最小值为( )
| A. | $\frac{π}{4}$ | B. | $\frac{3π}{8}$ | C. | $\frac{π}{2}$ | D. | π |
7.某驾校甲、乙、丙三名学员在考科目一前的10次模拟考试中通过的次数统计如表:
假设三名学员子啊正式考试中发挥正常,且各人成绩互不影响,将前10次模拟考试通过的频率作为正式考试通过的概率
(Ⅰ)求甲、乙、丙三名学员在正式考试中均未通过的概率
(Ⅱ)设甲、乙、丙三名学员在正式考试中通过的人数为ξ,求ξ的分布列及数学期望.
| 学员 | 甲 | 乙 | 丙 |
| 通过的次数 | 9 | 8 | 9 |
(Ⅰ)求甲、乙、丙三名学员在正式考试中均未通过的概率
(Ⅱ)设甲、乙、丙三名学员在正式考试中通过的人数为ξ,求ξ的分布列及数学期望.
1. 如图,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的右焦点,过F作渐近线的垂线,垂足为P,与另一条渐近线相交于Q,若|PF|=|PQ|,则C的离心率为( )
如图,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的右焦点,过F作渐近线的垂线,垂足为P,与另一条渐近线相交于Q,若|PF|=|PQ|,则C的离心率为( )
 如图,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的右焦点,过F作渐近线的垂线,垂足为P,与另一条渐近线相交于Q,若|PF|=|PQ|,则C的离心率为( )
如图,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的右焦点,过F作渐近线的垂线,垂足为P,与另一条渐近线相交于Q,若|PF|=|PQ|,则C的离心率为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{2}$ | C. | 2 | D. | $\sqrt{5}$ |
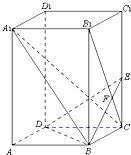 如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.
如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.