题目内容
16.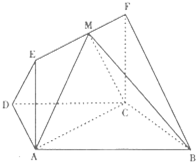 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.(1)求证:BC⊥平面ACFE.
(2)点M是线段EF上任意一点,求三棱锥B-ACM的体积.
分析 (1)先求得AB,利用勾股定理判断出BC⊥AC,利用线面垂直的判定定理证明出BC⊥平面ACFE.
(2)先求得△ACM的面积,进而利用体积公式求得答案.
解答 解:(1)在梯形ABCD中,
∵AB∥CD,AD=D=CB=1,∠ABC=60°,
∴AB=2,
∴AC2=AB2+BC2-2AB•BC•cos60°=3,
∴AB2=AC2+BC2,
∴BC⊥AC,
∵平面ACFE⊥平面ABCD,平面ACFE∩平面ABCD=AC,BC?平面ABCD,
∴BC⊥平面ACFE.
(2)∵四边形ACFE为矩形,
∴S△ACM=$\frac{1}{2}$AC•FC=$\frac{1}{2}$×$\sqrt{3}$×1=$\frac{\sqrt{3}}{2}$.
∵BC⊥平面ACFE.
∴VB-ACM=$\frac{1}{3}$S△ACM×BC=$\frac{\sqrt{3}}{6}$.
点评 本题主要考查了线面垂直的判定定理的运用.考查了学生的空间观察能力和计算能力.

练习册系列答案
相关题目
7.某驾校甲、乙、丙三名学员在考科目一前的10次模拟考试中通过的次数统计如表:
假设三名学员子啊正式考试中发挥正常,且各人成绩互不影响,将前10次模拟考试通过的频率作为正式考试通过的概率
(Ⅰ)求甲、乙、丙三名学员在正式考试中均未通过的概率
(Ⅱ)设甲、乙、丙三名学员在正式考试中通过的人数为ξ,求ξ的分布列及数学期望.
| 学员 | 甲 | 乙 | 丙 |
| 通过的次数 | 9 | 8 | 9 |
(Ⅰ)求甲、乙、丙三名学员在正式考试中均未通过的概率
(Ⅱ)设甲、乙、丙三名学员在正式考试中通过的人数为ξ,求ξ的分布列及数学期望.
11.若平面向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-2,y)且,则$\overrightarrow{a}⊥\overrightarrow{b}$,则|$\overrightarrow{b}$|=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{5}$ | C. | 2$\sqrt{2}$ | D. | 5 |
1. 如图,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的右焦点,过F作渐近线的垂线,垂足为P,与另一条渐近线相交于Q,若|PF|=|PQ|,则C的离心率为( )
如图,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的右焦点,过F作渐近线的垂线,垂足为P,与另一条渐近线相交于Q,若|PF|=|PQ|,则C的离心率为( )
 如图,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的右焦点,过F作渐近线的垂线,垂足为P,与另一条渐近线相交于Q,若|PF|=|PQ|,则C的离心率为( )
如图,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的右焦点,过F作渐近线的垂线,垂足为P,与另一条渐近线相交于Q,若|PF|=|PQ|,则C的离心率为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{2}$ | C. | 2 | D. | $\sqrt{5}$ |