题目内容
13.已知函数f(x)=sin(2ωx+$\frac{3}{5}$),且直线y=-1与函数交点之间的最短距离为$\frac{3}{π}$,求ω的值.分析 根据函数f(x)=sin(2ωx+$\frac{3}{5}$)的周期为$\frac{2π}{2ω}$=$\frac{3}{π}$,求得ω的值.
解答 解:由题意可得,函数f(x)=sin(2ωx+$\frac{3}{5}$)的周期为$\frac{2π}{2ω}$=$\frac{3}{π}$,求得ω=$\frac{{π}^{2}}{3}$.
点评 本题主要考查y=Asin(ωx+φ)的图象特征,y=Asin(ωx+φ)的周期性,属于基础题.

练习册系列答案
相关题目
3. 如图给出的是计算$\frac{1}{1}$+$\frac{1}{3}$+$\frac{1}{5}$+$\frac{1}{7}$+…+$\frac{1}{2015}$的一个程序框图,其中判断框内应填入的条件是( )
如图给出的是计算$\frac{1}{1}$+$\frac{1}{3}$+$\frac{1}{5}$+$\frac{1}{7}$+…+$\frac{1}{2015}$的一个程序框图,其中判断框内应填入的条件是( )
 如图给出的是计算$\frac{1}{1}$+$\frac{1}{3}$+$\frac{1}{5}$+$\frac{1}{7}$+…+$\frac{1}{2015}$的一个程序框图,其中判断框内应填入的条件是( )
如图给出的是计算$\frac{1}{1}$+$\frac{1}{3}$+$\frac{1}{5}$+$\frac{1}{7}$+…+$\frac{1}{2015}$的一个程序框图,其中判断框内应填入的条件是( )| A. | i<1008 | B. | i>1008 | C. | i<1009 | D. | i>1009 |
1. 如图,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的右焦点,过F作渐近线的垂线,垂足为P,与另一条渐近线相交于Q,若|PF|=|PQ|,则C的离心率为( )
如图,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的右焦点,过F作渐近线的垂线,垂足为P,与另一条渐近线相交于Q,若|PF|=|PQ|,则C的离心率为( )
 如图,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的右焦点,过F作渐近线的垂线,垂足为P,与另一条渐近线相交于Q,若|PF|=|PQ|,则C的离心率为( )
如图,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的右焦点,过F作渐近线的垂线,垂足为P,与另一条渐近线相交于Q,若|PF|=|PQ|,则C的离心率为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{2}$ | C. | 2 | D. | $\sqrt{5}$ |
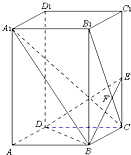 如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.
如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.