题目内容
如图是一个空间几何体的三视图,则该几何体的外接球的表面积为( )
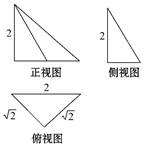
| A．8π | B．6π | C．4π | D．2π |
A
【思路点拨】该几何体是底面为等腰直角三角形,且一条侧棱垂直于底面的三棱锥,可将该几何体补成一个长方体,然后解决.
解：设该几何体的外接球的半径为R.
依题意知,该几何体是一个如图所示的三棱锥A-BCD,
其中AB⊥平面BCD,AB=2,BC=CD=
,BD=2,BC⊥DC,因此可将该三棱锥补成一个长方体,于是有(2R)2=22+()2+()2=8,即4R2=8,则该几何体的外接球的表面积为4πR2=8π.
解：设该几何体的外接球的半径为R.
依题意知,该几何体是一个如图所示的三棱锥A-BCD,
其中AB⊥平面BCD,AB=2,BC=CD=
,BD=2,BC⊥DC,因此可将该三棱锥补成一个长方体,于是有(2R)2=22+()2+()2=8,即4R2=8,则该几何体的外接球的表面积为4πR2=8π.
练习册系列答案
相关题目
的圆锥
中，已知
的直径
,
是
的中点，
是弦
的中点．
的平面角，并求出它的大小；
与
所成的角的正切值．
的正方形ABCD沿对角线BD折起，连结AC，得到三棱锥C-ABD，其正视图、俯视图均为全等的等腰直角三角形（如图所示），则其侧视图的面积为( )
πcm3
πcm3
πcm3
