题目内容

5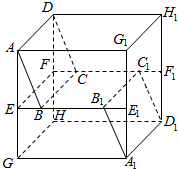．在棱长为40m的正方体AG1H1D-GA1D1H中，E、E1、F1、F分别是AG、G1A1、H1D1、DH的中点，B、B1是EE1上的点，C、C1是FF1上的点，且EB=E1B1=FC=F1C1=10m，求证：平面ABCD∥平面A1B1C1D1．

分析 由已知条件推导出AD∥A1D1，AB∥A1B1，由此能证明平面ABCD∥平面A1B1C1D1．

解答 证明：∵在棱长为40m的正方体AG1H1D-GA1D1H中，E、E1、F1、F分别是AG、G1A1、H1D1、DH的中点，
∴AD∥A1D1，
∵B、B1是EE1上的点，C、C1是FF1上的点，且EB=E1B1=FC=F1C1=10m，
∴AB∥A1B1，
∵AD∩AB=A，A1D1∩A1B1=A1，
AD?平面ABCD，AB?平面ABCD，A1D1?平面A1B1C1D1，A1B1?平面A1B1C1D1．
∴平面ABCD∥平面A1B1C1D1．

点评 本题考查面面平行的证明，是基础题，解题时要认真审题，注意空间思维能力的培养．

练习册系列答案
相关题目
6．当x∈[-2，2]时，函数f（x）=|x5-5x|的最大值为22．
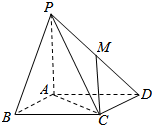16．如图，在四棱锥P-ABCD中，底面ABCD是边长为1的正方形，PA⊥底面ABCD，PA=AB，点M在棱PD上，PB∥平面ACM．
（1）试确定点M的位置，并说明理由；
（2）求四棱锥P-ABCD的表面积．
13．设F1、F2分别是双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点，P是C的右支上的点，射线PT平分∠F1PF2，过原点O做PT的平行线交PF1于点M，若|MP|=$\frac{1}{3}$|F1F2|，则C的离心率为$\frac{3}{2}$．
20．若函数f（x）=ax2+bx+c在x=-1，0，1三点处的函数值的绝对值均不大于1，当x∈[-1，1]时，求证：|ax+b|≤2．
10．已知直线y=$\frac{1}{2}$x+m经过双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$（a＞0，b＞0）的左焦点F，交y轴于点P，c为双曲线的半焦距，O为坐标原点，若|OP|，2a，|OF|成等比数列，求此双曲线的离心率和渐近线方程．
17．若p＞0，q＞0，p3+q3=2，求证：p+q≤2．
14．如图，过双曲线的右焦点F分别作两条渐近线的垂线，垂足为M、N，若$\overrightarrow{FM}$•$\overrightarrow{FN}$＜0，则此双曲线离心率的取值范围是（　　）
A．（1，$\sqrt{2}$）B．（1，2）C．（$\sqrt{2}$，+∞）D．（2，+∞）
15．已知（a2+b2）-abi与13+6i是共轭复数，求实数a，b的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网