题目内容
16．
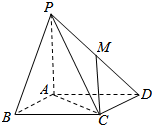如图，在四棱锥P-ABCD中，底面ABCD是边长为1的正方形，PA⊥底面ABCD，PA=AB，点M在棱PD上，PB∥平面ACM．（1）试确定点M的位置，并说明理由；
（2）求四棱锥P-ABCD的表面积．
分析 （1）设AC∩BD=O，则O是BD的中点，设点M为PD中点，在△PBD中，PB∥OM，由此能够确定M的位置使PB∥平面ACM．
（2）根据四棱锥P-ABCD中，底面ABCD是边长为1的正方形，PA⊥底面ABCD，PA=AB，可求四棱锥P-ABCD的表面积
解答 
解：（1）设AC∩BD=O，则O是BD的中点，
设点M为PD中点，
∵在△PBD中，PB∥OM，PB?平面ACM，OM?平面ACM，
∴PB∥平面ACM．
故当点M为PD中点时，PB∥平面ACM．
（2）∵四棱锥P-ABCD中，底面ABCD是边长为1的正方形，PA⊥底面ABCD，PA=AB，
∴四棱锥P-ABCD的表面积=1×1+2×$\frac{1}{2}×1×1$+2×$\frac{1}{2}×1×\sqrt{2}$=2+$\sqrt{2}$．
点评 本题考查满足条件的点的位置的确定，考查四棱锥P-ABCD的表面积的求法，属于中档题．
练习册系列答案
相关题目
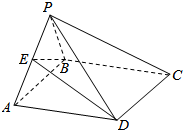如图，在四棱锥P-ABCD中，底面ABCD为平行四边形，平面PAB⊥平面ABCD，且PA=PB，E是PA的中点．
如图圆锥的轴截面为等腰直角三角形SAB，Q为底面圆周上一点．
如图，在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD为梯形，AD∥BC，且AB=2BC=4，PA=AD=3，∠ABC=60°，E是BC的中点．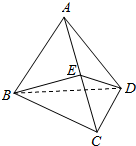
如图，平面ABC⊥平面BCD，AB=BC=BD=2，∠ABC=∠DBC=$\frac{π}{3}$，E为棱AD的中点．
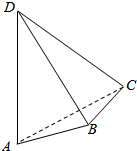如图，AD与BC是四面体ABCD中互相垂直的棱，若BC=2，AD=4，且∠ABD=∠ACD=60°，则四面体ABCD的体积的最大值是$\frac{4}{3}\sqrt{11}$．
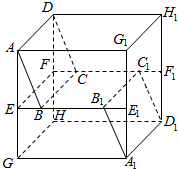在棱长为40m的正方体AG1H1D-GA1D1H中，E、E1、F1、F分别是AG、G1A1、H1D1、DH的中点，B、B1是EE1上的点，C、C1是FF1上的点，且EB=E1B1=FC=F1C1=10m，求证：平面ABCD∥平面A1B1C1D1．