题目内容
6.当x∈[-2,2]时,函数f(x)=|x5-5x|的最大值为22.分析 设g(x)=x5-5x,判断函数的奇偶性,求函数的导数,利用导数研究函数在[0,2]上的最值,即可得到结论.
解答 解:设g(x)=x5-5x,则g(-x)=-x5+5x=-(x5-5x)=-g(x),
则g(x)为奇函数,
则当0≤x≤2时,g′(x)=5x4-5=5(x4-1)=5(x2+1)(x2-1),
由g′(x)>0得x>1或x<-1,即此时1<x≤2时,函数g(x)为增函数,
g′(x)<0得-1<x<1,即此时0≤x<1时,函数g(x)为减函数,
即当x=1时,函数取得极小值,同时也是最小值,g(1)=1-5=-4,
∵g(0)=0,g(2)=25-5×2=32-10=22,
∴在[0,2]上的最大值为22,即当0≤x≤2时,-4≤g(x)≤22,
则0≤|g(x)|≤22
∴x∈[-2,2]时,函数f(x)=|x5-5x|的最大值为22,
故答案为:22
点评 本题主要考查函数最值的求解,构造函数,利用函数的奇偶性以及函数单调性和导数之间是关系求出函数的最值是解决本题的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案
相关题目
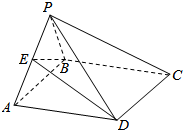 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,平面PAB⊥平面ABCD,且PA=PB,E是PA的中点.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,平面PAB⊥平面ABCD,且PA=PB,E是PA的中点. 如图圆锥的轴截面为等腰直角三角形SAB,Q为底面圆周上一点.
如图圆锥的轴截面为等腰直角三角形SAB,Q为底面圆周上一点. 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为梯形,AD∥BC,且AB=2BC=4,PA=AD=3,∠ABC=60°,E是BC的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为梯形,AD∥BC,且AB=2BC=4,PA=AD=3,∠ABC=60°,E是BC的中点.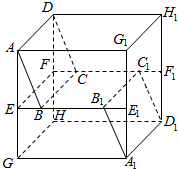 在棱长为40m的正方体AG1H1D-GA1D1H中,E、E1、F1、F分别是AG、G1A1、H1D1、DH的中点,B、B1是EE1上的点,C、C1是FF1上的点,且EB=E1B1=FC=F1C1=10m,求证:平面ABCD∥平面A1B1C1D1.
在棱长为40m的正方体AG1H1D-GA1D1H中,E、E1、F1、F分别是AG、G1A1、H1D1、DH的中点,B、B1是EE1上的点,C、C1是FF1上的点,且EB=E1B1=FC=F1C1=10m,求证:平面ABCD∥平面A1B1C1D1.