题目内容
17．若p＞0，q＞0，p3+q3=2，求证：p+q≤2．分析 利用反证法证明，假设p+q＞2，通过p＞2-q可知p3＞（2-q）3，代入p3+q3=2整理可知（q-1）2＜0，得出矛盾，进而可得结论．
解答 证明：假设p+q＞2，则p＞2-q，
∴p3＞（2-q）3，
整理得：p3+q3＞8-12q+6q2，
又∵p3+q3=2，
∴2＞8-12q+6q2，即q2-2q+1＜0，
∴（q-1）2＜0，矛盾，
即p+q≤2．
点评 本题考查不等式的证明，利用反证法是解决本题的关键，注意解题方法的积累，属于中档题．
练习册系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
如图圆锥的轴截面为等腰直角三角形SAB，Q为底面圆周上一点．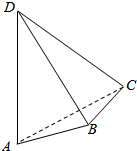
如图，AD与BC是四面体ABCD中互相垂直的棱，若BC=2，AD=4，且∠ABD=∠ACD=60°，则四面体ABCD的体积的最大值是$\frac{4}{3}\sqrt{11}$．
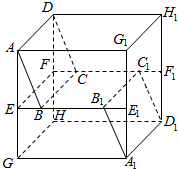在棱长为40m的正方体AG1H1D-GA1D1H中，E、E1、F1、F分别是AG、G1A1、H1D1、DH的中点，B、B1是EE1上的点，C、C1是FF1上的点，且EB=E1B1=FC=F1C1=10m，求证：平面ABCD∥平面A1B1C1D1．
12．某地区汽车限行规定如下：
某地区某行政单位有车牌尾号为6的汽车A和尾号为9的汽车B，在非限行日，A车日出车频率为p，B车日出车频率为q，周六、周日和限行日停止用车，现将汽车日出车频率视为日出车概率，且A，B两车是否出车相互独立．
（1）若p=0.8，求汽车A在同一周内恰有两天连续出车的概率；
（2）若p∈[0.4，0.8]，且两车的日出车频率之和为1，为实现节能减排与绿色出行，应如何调控两车的日出车频率，使得一周内汽车A，B同日都出车的平均天数最少．
| 车尾号 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
| 限行日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
（1）若p=0.8，求汽车A在同一周内恰有两天连续出车的概率；
（2）若p∈[0.4，0.8]，且两车的日出车频率之和为1，为实现节能减排与绿色出行，应如何调控两车的日出车频率，使得一周内汽车A，B同日都出车的平均天数最少．
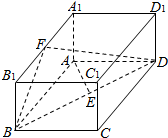如图，已知在长方体ABCD-A1B1C1D1中，AB=2，AA1=1，直线BD与平面AA1B1B所成的角为30°，AE垂直BD于点E，F为A1B1的中点．