Question

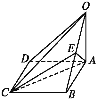
【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90°,E是CD的中点.

求证:CD⊥平面PAE.

Answer 1

【答案】见解析

【解析】

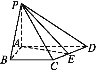
如图,以A为坐标原点,AB,AD,AP所在直线分别为x轴、y轴、z轴建立空间直角坐标系.设PA=h,则A(0,0,0),B(4,0,0),C(4,3,0),D(0,5,0),E(2,4,0),P(0,0,h).

则利用空间向量证明CD⊥AE,CD⊥A.即可.

证明：如图,以A为坐标原点,AB,AD,AP所在直线分别为x轴、y轴、z轴建立空间直角坐标系.

设PA=h,则A(0,0,0),B(4,0,0),C(4,3,0),D(0,5,0),E(2,4,0),P(0,0,h).

易知=(-4,2,0),=(2,4,0),=(0,0,h).

∵=-8+8+0=0,=0,∴CD⊥AE,CD⊥AP.

∵AP∩AE=A,∴CD⊥平面PAE.