题目内容
【题目】如图,在底面为平行四边形的四棱锥O-ABCD中,BC⊥平面OAB,E为OB中点,OA=AD=2AB=2,OB=![]() .
.
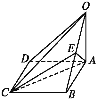
(1)求证:平面OAD⊥平面ABCD;
(2)求二面角B-AC-E的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据已知条件,判断出OA⊥BC与OA⊥AB,进而判断平面和平面的垂直。
(2)建立空间直角坐标系,写出各个点的坐标,求出两个平面的法向量,进而利用两个平面的法向量求出两个平面的二面角大小。
(1)证明∵BC⊥平面OAB,OA平面OAB,
∴OA⊥BC.又OA=2AB=2,OB=![]() ,
,
在△OAB中,OA2+AB2=OB2,
∴OA⊥AB,∴OA⊥平面ABCD.
又OA平面OAD,∴平面OAD⊥平面ABCD.
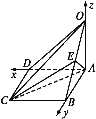
(2)解由(1)知OA,AB,AD两两垂直,以A为坐标原点,分别以AD,AB,AO所在直线为x轴,y轴,z轴,建立空间直角坐标系
,则A(0,0,0),C(2,1,0),O(0,0,2),B(0,1,0),E![]() =(2,1,0),
=(2,1,0),![]() .
.
设平面AEC的法向量n=(x,y,z),
则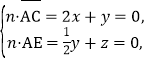
取x=1,得n=(1,-2,1).
又平面ABC的法向量m=(0,0,1),
cos<m,n>=![]() .
.
∴二面角B-AC-E的余弦值为![]() .
.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目