Question

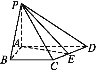
【题目】如图，在三棱锥P﹣ABC中，PA⊥AB，PA⊥BC，AB⊥BC，PA=AB=BC=2，D为线段AC的中点，E为线段PC上一点．

（1）求证：PA⊥BD；
（2）求证：平面BDE⊥平面PAC；
（3）当PA∥平面BDE时，求三棱锥E﹣BCD的体积．

Answer 1

【答案】
（1）

解：证明：由PA⊥AB，PA⊥BC，

AB平面ABC，BC平面ABC，且AB∩BC=B，

可得PA⊥平面ABC，

由BD平面ABC，

可得PA⊥BD；

（2）

解：证明：由AB=BC，D为线段AC的中点，

可得BD⊥AC，

由PA⊥平面ABC，PA平面PAC，

可得平面PAC⊥平面ABC，

又平面ABC∩平面ABC=AC，

BD平面ABC，且BD⊥AC，

即有BD⊥平面PAC，

BD平面BDE，

可得平面BDE⊥平面PAC；

（3）

解：PA∥平面BDE，PA平面PAC，

且平面PAC∩平面BDE=DE，

可得PA∥DE，

又D为AC的中点，

可得E为PC的中点，且DE= PA=1，

由PA⊥平面ABC，

可得DE⊥平面ABC，

可得S△BDC= S△ABC= × ×2×2=1，

则三棱锥E﹣BCD的体积为 DES△BDC= ×1×1= ．

【解析】（1.）运用线面垂直的判定定理可得PA⊥平面ABC，再由性质定理即可得证；
（2.）要证平面BDE⊥平面PAC，可证BD⊥平面PAC，由（1）运用面面垂直的判定定理可得平面PAC⊥平面ABC，再由等腰三角形的性质可得BD⊥AC，运用面面垂直的性质定理，即可得证；
（3.）由线面平行的性质定理可得PA∥DE，运用中位线定理，可得DE的长，以及DE⊥平面ABC，求得三角形BCD的面积，运用三棱锥的体积公式计算即可得到所求值．
【考点精析】通过灵活运用直线与平面垂直的判定和直线与平面垂直的性质，掌握一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想；垂直于同一个平面的两条直线平行即可以解答此题．