题目内容
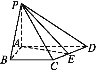
【题目】如图所示,A,B分别是椭圆C:
=1(a>b>0)的左右顶点,F为其右焦点,2是|AF|与|FB|的等差中项,
是|AF|与|FB|的等比中项.点P是椭圆C上异于A,B的任一动点,过点A作直线l⊥x轴.以线段AF为直径的圆交直线AP于点A,M,连接FM交直线l于点Q.
(1)求椭圆C的方程;
(2)试问在x轴上是否存在一个定点N,使得直线PQ必过该定点N?若存在,求出点N的坐标,若不存在,说明理由.
【答案】（1）
；（2）见解析
【解析】
(1)根据题意，用a、c表示出|AF|、|FB，再根据等差中项与等比中项定义求出a、b、c，进而求得椭圆方程。
(2)假设存在这样的定点。设出动点P，由P再椭圆上，用x0表示y0，再表示出FM的方程，联立FM与直线
，得交点Q，进而求得过定点的坐标。
(1)由题意得|AF|=a+c,|FB|=a-c,
即
解得a=2,c=1,∴b2=4-1=3.
∴所求椭圆的方程为
=1.
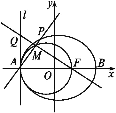
(2)假设在x轴上存在一个定点N(n,0),使得直线PQ必过定点N(n,0).
设动点P(x0,y0),由于P点异于A,B,故y0≠0,
由点P在椭圆上,故有
=1,
∴
. ①
又由(1)知A(-2,0),F(1,0),
∴直线AP的斜率kAP=
.
又点M是以线段AF为直径的圆与直线AP的交点,∴AP⊥FM.
∴kAP·kMF=-1kMF=-
=-
.
∴直线FM的方程y=-(x-1).
联立FM,l的方程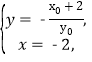
得交点Q
.
∴P,Q两点连线的斜率kPQ=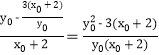
, ②
将①式代入②式,并整理得kPQ=
,
又P,N两点连线的斜率kPN=
.
若直线QP必过定点N(n,0),则必有kPQ=kPN恒成立,即
,
整理得4
=-3(x0+2)(x0-n), ③
将①式代入③式,得4×
=-3(x0+2)(x0-n),解得n=2,故直线PQ过定点(2,0).
