题目内容
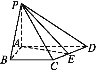
【题目】如图所示,在四面体ABCD中,AB,BC,CD两两互相垂直,且BC=CD=1.
(1)求证:平面ACD⊥平面ABC;
(2)求二面角C-AB-D的大小;
【答案】(1)见解析;(2)![]()
【解析】
(1)CD⊥AB,CD⊥BC,可得CD⊥平面ABC,从而有平面ACD⊥平面ABC。
(2)建立空间坐标系,求出平面ABC的法向量![]() =(1,0,0)和平面ABD的一个法向量为(-1,1,0),代入计算公式即可。
=(1,0,0)和平面ABD的一个法向量为(-1,1,0),代入计算公式即可。
(1)证明因为CD⊥AB,CD⊥BC,
所以CD⊥平面ABC.
又因为CD平面ACD,
故平面ACD⊥平面ABC.
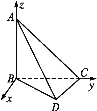
(2)解设AB=a,建立如图所示的空间直角坐标系Bxyz,
则B(0,0,0),A(0,0,a),C(0,1,0),D(1,1,0),于是![]() =(1,1,0),
=(1,1,0),![]() =(0,0,a).
=(0,0,a).
显然平面ABC的法向量![]() =(1,0,0).
=(1,0,0).
设平面ABD的一个法向量为n=(x,y,z),
则有![]() ·n=x+y=0,
·n=x+y=0,![]() ·n=az=0,
·n=az=0,
所以z=0,取y=1,则x=-1,则n=(-1,1,0).
因此cos<![]() ,n>=
,n>=![]() =-
=-![]() ,
,
由图可知二面角C-AB-D为锐角,所以二面角C-AB-D的大小为45°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目