题目内容
【题目】设函数f(x)=ex﹣ax+a(a∈R),其图象与x轴交于A(x1,0),B(x2,0)两点,且x1<x2.
(1)求a的取值范围;
(2)证明:f′(![]() )<0(f′(x)为函数f(x)的导函数);
)<0(f′(x)为函数f(x)的导函数);
(3)设点C在函数y=f(x)的图象上,且△ABC为等腰直角三角形,记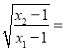 t,求(a﹣1)(t﹣1)的值.
t,求(a﹣1)(t﹣1)的值.
【答案】(1)见解析; (2)见解析(3)2
【解析】
(1)∵f(x)=ex﹣ax+a,
∴f'(x)=ex﹣a,
若a≤0,则f'(x)>0,则函数f(x)是单调增函数,这与题设矛盾.
∴a>0,令f'(x)=0,则x=lna,
当f'(x)<0时,x<lna,f(x)是单调减函数,
当f'(x)>0时,x>lna,f(x)是单调增函数,
于是当x=lna时,f(x)取得极小值,
∵函数f(x)=ex﹣ax+a(a∈R)的图象与x轴交于两点A(x1,0),B(x2,0)(x1<x2),
∴f(lna)=a(2﹣lna)<0,即a>e2,
此时,存在1<lna,f(1)=e>0,
存在3lna>lna,f(3lna)=a3﹣3alna+a>a3﹣3a2+a>0,
又由f(x)在(﹣∞,lna)及(lna,+∞)上的单调性及曲线在R上不间断,
可知a>e2为所求取值范围.
(2)∵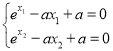 ,
,
∴两式相减得![]() .
.
记![]() ,则
,则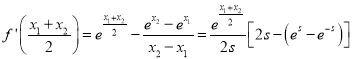 ,
,
设g(s)=2s﹣(es﹣e﹣s),
则g'(s)=2﹣(es+e﹣s)<0,
∴g(s)是单调减函数,
则有g(s)<g(0)=0,而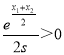 ,
,
∴![]() .
.
又f'(x)=ex﹣a是单调增函数,且![]()
∴![]() .
.
(3)依题意有![]() ,则
,则![]() xi>1(i=1,2).
xi>1(i=1,2).
于是![]() ,在等腰三角形ABC中,显然C=90°,
,在等腰三角形ABC中,显然C=90°,
∴![]() ,即y0=f(x0)<0,
,即y0=f(x0)<0,
由直角三角形斜边的中线性质,可知![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
即![]() .
.
∵x1﹣1≠0,则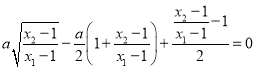 ,
,
又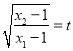 ,
,
∴![]() ,
,
即![]() ,
,
∴(a﹣1)(t﹣1)=2.

 名校课堂系列答案
名校课堂系列答案【题目】“未来肯定是非接触的,无感支付的方式将成为主流,这有助于降低交互门槛”.云从科技联合创始人姚志强告诉南方日报记者.相对于主流支付方式二维码支付,刷脸支付更加便利,以前出门一部手机解决所有,而现在连手机都不需要了,毕竟,手机支付还需要携带手机,打开二维码也需要时间和手机信号.刷脸支付将会替代手机,成为新的支付方式.某地从大型超市门口随机抽取50名顾客进行了调查,得到了如下列联表:
男性 | 女性 | 总计 | |
刷脸支付 | 18 | 25 | |
非刷脸支付 | 13 | ||
总计 | 50 |
(1)请将上面的列联表补充完整,并判断是否有95%的把握认为使用刷脸支付与性别有关?
(2)从参加调查且使用刷脸支付的顾客中随机抽取2人参加抽奖活动,抽奖活动规则如下:
“一等奖”中奖概率为0.25,奖品为10元购物券![]() 张(
张(![]() ,且
,且![]() ),“二等奖”中奖概率0.25,奖品为10元购物券两张,“三等奖”中奖概率0.5,奖品为10元购物券一张,每位顾客是否中奖相互独立,记参与抽奖的两位顾客中奖购物券金额总和为
),“二等奖”中奖概率0.25,奖品为10元购物券两张,“三等奖”中奖概率0.5,奖品为10元购物券一张,每位顾客是否中奖相互独立,记参与抽奖的两位顾客中奖购物券金额总和为![]() 元,若要使
元,若要使![]() 的均值不低于50元,求
的均值不低于50元,求![]() 的最小值.
的最小值.
附: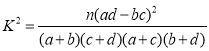 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.869 |