题目内容
【题目】在平面直角坐标系中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,两种坐标系中取相同的长度单位.已知直线l的参数方程为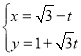 (t为参数),曲线C的极坐标方程为ρ=4sin(θ+
(t为参数),曲线C的极坐标方程为ρ=4sin(θ+![]() ).
).
(1)求直线l的普通方程与曲线C的直角坐标方程;
(2)若直线l与曲线C交于M,N两点,求△MON的面积.
【答案】(1) 直线l的普通方程为![]() x+y-4=0. 曲线C的直角坐标方程是圆:(x-
x+y-4=0. 曲线C的直角坐标方程是圆:(x-![]() )2+(y-1)2=4. (2)4
)2+(y-1)2=4. (2)4
【解析】
(1)将直线l参数方程中的![]() 消去,即可得直线l的普通方程,对曲线C的极坐标方程两边同时乘以
消去,即可得直线l的普通方程,对曲线C的极坐标方程两边同时乘以![]() ,利用
,利用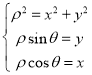 可得曲线C的直角坐标方程;
可得曲线C的直角坐标方程;
(2)求出点![]() 到直线的距离,再求出
到直线的距离,再求出![]() 的弦长,从而得出△MON的面积.
的弦长,从而得出△MON的面积.
解:(1)由题意有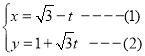 ,
,
![]() 得,
得,
![]() x+y=4,
x+y=4,
直线l的普通方程为![]() x+y-4=0.
x+y-4=0.
因为ρ=4sin![]()
所以ρ=2sinθ+2![]() cosθ,
cosθ,
两边同时乘以![]() 得,
得,
ρ2=2ρsinθ+2![]() ρcosθ,
ρcosθ,
因为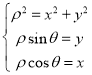 ,
,
所以x2+y2=2y+2![]() x,即(x-
x,即(x-![]() )2+(y-1)2=4,
)2+(y-1)2=4,
∴曲线C的直角坐标方程是圆:(x-![]() )2+(y-1)2=4.
)2+(y-1)2=4.
(2)∵原点O到直线l的距离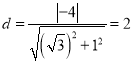
直线l过圆C的圆心(![]() ,1),
,1),
∴|MN|=2r=4,
所以△MON的面积S=![]() |MN|×d=4.
|MN|×d=4.

练习册系列答案
相关题目