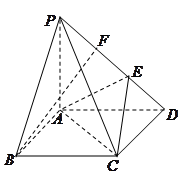题目内容
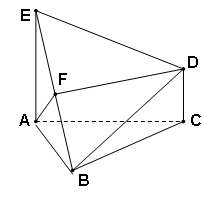
((本题满分14分)已知,如图四棱锥P—ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上,且AG= GD,BG⊥GC,GB=GC=2,E是BC的中点,四面体P—BCG的体积为
GD,BG⊥GC,GB=GC=2,E是BC的中点,四面体P—BCG的体积为 .(Ⅰ)求异面直线GE与PC所成角的余弦;(Ⅱ)求点D到平面PBG的距离;(Ⅲ)若F点是棱PC上一点,且DF⊥GC,求
.(Ⅰ)求异面直线GE与PC所成角的余弦;(Ⅱ)求点D到平面PBG的距离;(Ⅲ)若F点是棱PC上一点,且DF⊥GC,求 的值.
的值.

 GD,BG⊥GC,GB=GC=2,E是BC的中点,四面体P—BCG的体积为
GD,BG⊥GC,GB=GC=2,E是BC的中点,四面体P—BCG的体积为 .(Ⅰ)求异面直线GE与PC所成角的余弦;(Ⅱ)求点D到平面PBG的距离;(Ⅲ)若F点是棱PC上一点,且DF⊥GC,求
.(Ⅰ)求异面直线GE与PC所成角的余弦;(Ⅱ)求点D到平面PBG的距离;(Ⅲ)若F点是棱PC上一点,且DF⊥GC,求 的值.
的值.
解:(I)由已知
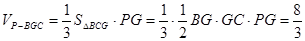
∴PG=4 ………4分
如图所示,以G点为原点建立空间直角坐标系
o—xyz,则
B(2,0,0),C(0,2,0),P(0,0,4)
故E(1,1,0)

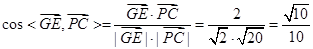 ∴异面直线GE与PC所成角的余弦为
∴异面直线GE与PC所成角的余弦为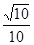 ……6分
……6分(II)平面PBG的单位法向量
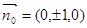

∴点D到平面PBG的距离为
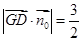 ………10分
………10分(III)设F(0,y , z)
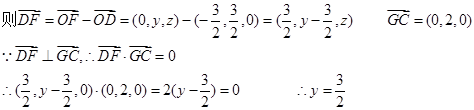
在平面PGC内过F点作FM⊥GC,M为垂足,则
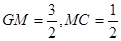

………14分
略

练习册系列答案
相关题目
 的高为
的高为 ,若三个侧面两两垂直,则
,若三个侧面两两垂直,则 为△
为△ 的( )
的( )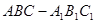 中,
中,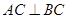 ,
,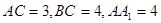 ,点
,点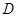 是
是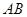 的中点,
的中点,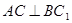 ;
;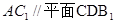 ;
;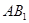 与平面
与平面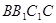 所成角的正切值.
所成角的正切值.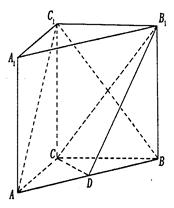

 平面
平面 ,平面
,平面 //直线
//直线 ,则
,则 //
//
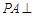 矩形
矩形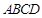 所在平面,
所在平面,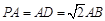 ,
,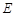 为线段
为线段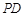 上一点,
上一点,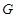 为线段
为线段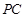
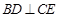 ;
;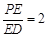 时,求证:BG//平面AEC.
时,求证:BG//平面AEC.
 的顶点
的顶点 ,引
,引 ⊥平面
⊥平面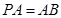 ,则平面ABCD和平面
,则平面ABCD和平面 所成的二面角的大小是
所成的二面角的大小是


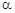 、
、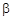 是两个不同的平面,则下列命题正确的是( )
是两个不同的平面,则下列命题正确的是( )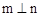 、 m
、 m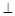
 ∥n
∥n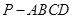 的底面是边长为1的正方形,
的底面是边长为1的正方形,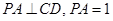 ,
,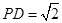 ,
, 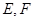 为
为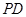 上两点,且
上两点,且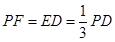 .
.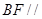 面
面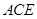 ;
;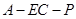 的正切值.
的正切值.