题目内容
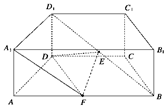
(本小题满分12分)如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点,求证:

(1) FD∥平面ABC;
(2)AF⊥平面EDB.
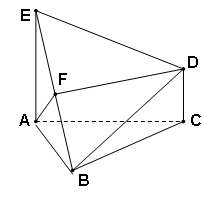

(1) FD∥平面ABC;
(2)AF⊥平面EDB.

证明 (1)取AB的中点M,连FM,MC,
∵ F、M分别是BE、BA的中点
∴ FM∥EA, FM=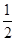 EA
EA
∵ EA、CD都垂直于平面ABC
∴ CD∥EA∴ CD∥FM
又 DC="a, " ∴ FM="DC " ∴四边形FMCD是平行四边形
∴ FD∥MC ∴ FD∥平面ABC……………………………………6分
(2)因M是AB的中点,△ABC是正三角形,所以CM⊥AB
又 CM⊥AE,所以CM⊥面EAB, CM⊥AF, FD⊥AF,
因F是BE的中点, EA=AB所以AF⊥EB. …………………12分
∵ F、M分别是BE、BA的中点
∴ FM∥EA, FM=
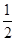 EA
EA∵ EA、CD都垂直于平面ABC
∴ CD∥EA∴ CD∥FM
又 DC="a, " ∴ FM="DC " ∴四边形FMCD是平行四边形
∴ FD∥MC ∴ FD∥平面ABC……………………………………6分
(2)因M是AB的中点,△ABC是正三角形,所以CM⊥AB
又 CM⊥AE,所以CM⊥面EAB, CM⊥AF, FD⊥AF,
因F是BE的中点, EA=AB所以AF⊥EB. …………………12分
略

练习册系列答案
相关题目
 GD,BG⊥GC,GB=GC=2,E是BC的中点,四面体P—BCG的体积为
GD,BG⊥GC,GB=GC=2,E是BC的中点,四面体P—BCG的体积为 .(Ⅰ)求异面直线GE与PC所成角的余弦;(Ⅱ)求点D到平面PBG的距离;(Ⅲ)若F点是棱PC上一点,且DF⊥GC,求
.(Ⅰ)求异面直线GE与PC所成角的余弦;(Ⅱ)求点D到平面PBG的距离;(Ⅲ)若F点是棱PC上一点,且DF⊥GC,求 的值.
的值.
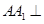 平面
平面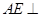 平面A1BD;
平面A1BD;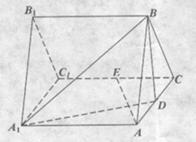
 是矩形,平面
是矩形,平面 平面
平面 ,已知
,已知 ,
, ,且当规定主(正)视方向垂直平面
,且当规定主(正)视方向垂直平面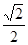 .若
.若 、
、 分别是线段
分别是线段 、
、 上的动点,则
上的动点,则

 的边长为1,
的边长为1,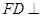 平面
平面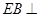 平面
平面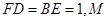 为
为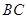 边上的动点。
边上的动点。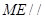 平面
平面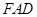 ;
; 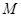 的位置,使平面
的位置,使平面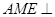 平面
平面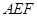 。
。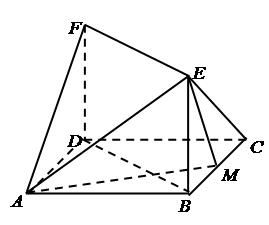
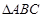 中,
中, ,垂足为
,垂足为 ,且
,且 .
.  的大小;
的大小; 为
为 的中点,已知
的中点,已知 的长
的长 
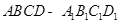 的棱长为
的棱长为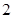 ,
,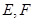 分别为棱
分别为棱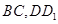 上的点,给出下列命题:
上的点,给出下列命题: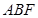 内总存在与直线
内总存在与直线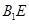 平行的直线;
平行的直线;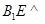 平面
平面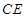 与
与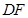 的长度之和为
的长度之和为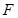 使二面角
使二面角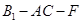 的大小为
的大小为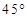 ;
;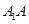 与平面
与平面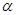 ,
,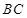 与平面
与平面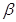 ,则
,则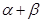 的大小与点
的大小与点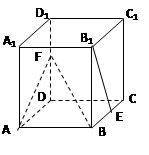
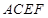 的边
的边 与正方形
与正方形 所在平面垂直,
所在平面垂直,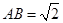 ,
,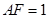 ,
,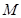 是线段
是线段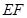 的中点。
的中点。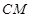 与直线
与直线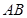 所成的角的大小;
所成的角的大小;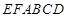 的表面积。
的表面积。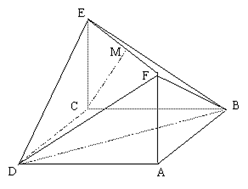
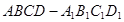 中,底面
中,底面 是等腰梯形,
是等腰梯形,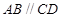 ,
,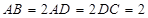 ,
,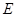 为
为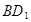 的中点,
的中点, 为
为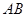 中点.
中点.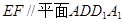 ;
;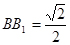 ,求
,求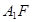 与平面
与平面 所成角的正弦值.
所成角的正弦值.