题目内容
4.直线2ρcosθ=1与圆ρ=2cosθ相交的弦长为$\sqrt{3}$.分析 化极坐标方程为直角坐标方程,然后由直线和圆的位置关系求得弦长.
解答 解:由2ρcosθ=1,可得直线方程为x=$\frac{1}{2}$,
由ρ=2cosθ,得ρ2=2ρcosθ,即x2+y2=2x,化为标准方程得(x-1)2+y2=1.
如图,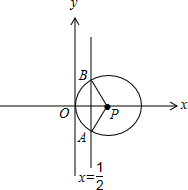
∴弦AB的长为$2×\sqrt{{1}^{2}-(\frac{1}{2})^{2}}=\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查了简单曲线的极坐标方程,考查了直线和圆的位置关系,是基础的计算题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.若复数z满足(3-4i)z=|4+3i|,则z的虚部为( )
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$i | C. | $\frac{4}{5}$i | D. | 4 |
13.已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上是减函数,若$f({ln\frac{n}{m}})-f(1)>0$,则$\frac{{{m^2}+{n^2}}}{mn}$的取值范围是( )
| A. | [2,+∞) | B. | [2,e) | C. | $({e+\frac{1}{e},+∞})$ | D. | $[{2,e+\frac{1}{e}})$ |