题目内容
【题目】已知函数![]() 的最大值为
的最大值为![]() (其中
(其中![]() 为自然对数的底数),
为自然对数的底数),![]() 是
是![]() 的导函数。
的导函数。
(1)求![]() 的值;
的值;
(2)任取两个不等的正数![]() ,且
,且![]() ,若存在正数
,若存在正数![]() ,使得
,使得![]() 成立。求证:
成立。求证:![]() 。
。
【答案】(1)![]() .(2)见解析.
.(2)见解析.
【解析】
(1)对函数求导,分情况得到函数的单调性,进而求得在![]() 处取得最值,进而求解;(2)根据导数的几何意义得到
处取得最值,进而求解;(2)根据导数的几何意义得到![]() ,构造函数
,构造函数![]() ,通过换元将等式右边的函数改为
,通过换元将等式右边的函数改为![]() ,对此函数求导得到函数的单调性进而得证.
,对此函数求导得到函数的单调性进而得证.
(1)由题意得,显然![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
令![]() ,解得
,解得![]() ,
,
①.当![]() 时,令
时,令![]() ,解得
,解得![]() ;令
;令![]() ,解得
,解得![]() ,
,
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
∴![]() 在
在![]() 处取得极大值,也是最大值,
处取得极大值,也是最大值,
∴![]() ,解得
,解得![]() ;
;
②当![]() 时,易知与题意不符,故舍去,
时,易知与题意不符,故舍去,
综上所述,![]() ;
;
(2)由(1)知![]() ,则
,则![]() ,∴
,∴![]() ,
,
∴![]() ,即
,即![]() ,
,
则![]()
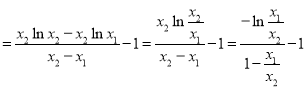 ,
,
设![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,
,
∴函数![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() ,即
,即![]() ,又
,又![]() ,
,
∴![]() ,即
,即![]() ,∴
,∴![]() ,
,
同理可证![]() ,得证。
,得证。

练习册系列答案
相关题目
【题目】某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
积极参加 班级工作 | 不太主动参加 班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性一般 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法能否有99.9%的把握认为学生的学习积极性与对待班级工作的态度有关系?并说明理由.(参考下表)
P(K2 ≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: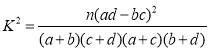 ,其中
,其中![]() )
)