Question

【题目】已知函数有三个极值点，

（1）求实数的取值范围；

（2）求证：.

Answer 1

【答案】（1）且；（2）证明见解析.

【解析】

（1）函数有3个零点等价于有3个变号零点，由于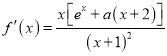，且，所以可得有两个不为0，－1的实根，再对求导讨论其单调性可得结果；

（2）由（1）可知有一个零点为0，所以不妨设，，而，所以，因此要证，即证而，，而在上递减，，所以只需证，即，然后构造函数，只需证此函数值恒大于零即可.

解：（1）利用的极值点个数即为的变号零点个数

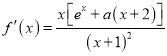，，设，

由已知，方程有两个不为0，－1的实根，

当时，在上递增，至多一个实根，故

所以在上递减，在上递增，

因为，

所以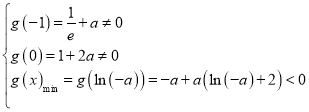时，有两个实根，

解得且

（2）由（1）不妨设，，∵，∴.

要证，即证而，

由在上递减，在上递增，且

故只要证，又，故只要证

即证

设

∴

∴递增，∴

即

∴