题目内容
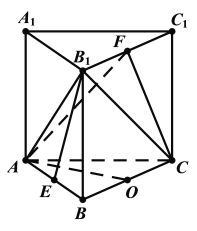
【题目】如图，在正三棱柱
中，
，E，F分别为AB，
的中点.
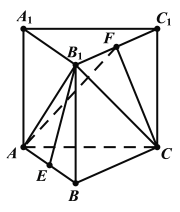
（1）求证：
平面ACF；
（2）求三棱锥
的体积.
【答案】（1）证明见解析；（2）
.
【解析】
（1）取AC的中点M，连结EM，FM，然后利用三角形中位线定理，再结合正棱柱的性质，可得四边形
为平行四边形，从而可得
，再由线面平行定理可证得结果.
（2）设O为BC的中点，则可证得
平面
，所以
，然后代入值计算即可.
（1）证明：取AC的中点M，连结EM，FM，
在
中，因为E、M分别为AB，AC的中点，
所以
且
又F为
的点，
，
所以
且
，
即
且
，
故四边形为平行四边形，所以.
又
平面ACF内，
在平面ACF外，
所以
平面ACF.
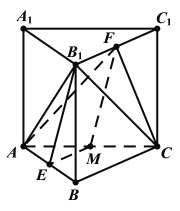
（2）设O为BC的中点，因棱柱底面是正三角形，
所以有
，且
，
因为正三棱柱
，
所以
平面ABC，
在平面ABC内，所以
，
因为
，
在平面内，
所以平面.
于是
.
练习册系列答案
相关题目
【题目】
大学生是国家的未来，代表着国家可持续发展的实力，能够促进国家综合实力的提高.据统计，2016年至2020年我国高校毕业生人数y(单位：万人)的数据如下表：
年份 | 2016 | 2017 | 2018 | 2019 | 2020 |
年份代号x | 16 | 17 | 18 | 19 | 20 |
高校毕业生人数y(单位：万人) | 765 | 795 | 820 | 834 | 874 |
（1）根据上表数据，计算y与x的相关系数r，并说明y与x的线性相关性的强弱.
(已知：
，则认为y与x线性相关性很强；
，则认为y与x线性相关性一般；
，则认为y与x线性相关性较弱)
（2）求y关于x的线性回归方程，并预测2022年我国高校毕业生的人数(结果取整数).
参考公式和数据：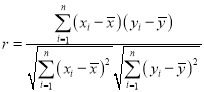
，
，
，
，
，
.
