题目内容
【题目】一款小游戏的规则如下:每轮游戏要进行三次,每次游戏都需要从装有大小相同的2个红球,3个白球的袋中随机摸出2个球,若摸出的“两个都是红球”出现3次获得200分,若摸出“两个都是红球”出现1次或2次获得20分,若摸出“两个都是红球”出现0次则扣除10分(即获得![]() 分).
分).
(1)设每轮游戏中出现“摸出两个都是红球”的次数为![]() ,求
,求![]() 的分布列;
的分布列;
(2)玩过这款游戏的许多人发现,若干轮游戏后,与最初的分数相比,分数没有增加反而减少了,请运用概率统计的相关知识分析解释上述现象.
【答案】(1)分布列见解析;(2)见解析
【解析】
(1)求出每次游戏,出现“两个都是红球”的概率为![]() ,再根据二项分布可求得
,再根据二项分布可求得![]() 的分布列;
的分布列;
(2)设每轮游戏得分为![]() ,进而求出
,进而求出![]() 的期望值为负数,即可得到结论.
的期望值为负数,即可得到结论.
(1)每次游戏,出现“两个都是红球”的概率为![]() .
.
![]() 可能的取值为0,1,2,3,
可能的取值为0,1,2,3,
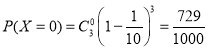 ,
,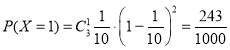 ,
,
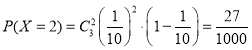 ,
,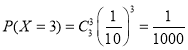 ,
,
所以![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
(2)设每轮游戏得分为![]() .
.
由(1)知,![]() 的分布列为:
的分布列为:
|
| 20 | 200 |
|
|
|
|
![]() 的数学期望为
的数学期望为![]() .
.
这表明,获得分数![]() 的期望为负.因此,多次游戏之后大多数人的分数减少了.
的期望为负.因此,多次游戏之后大多数人的分数减少了.

练习册系列答案
相关题目