Question

【题目】已知圆M的圆心M在y轴上，半径为1．直线l：y=2x+2被圆M所截得的弦长为 ，且圆心M在直线l的下方．
（1）求圆M的方程；
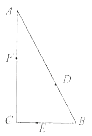
（2）设A（t，0），B（t+5，0）（﹣4≤t≤﹣1），若AC，BC是圆M的切线，求△ABC面积的最小值．

Answer 1

【答案】
（1）解：设M（0，b）由题设知，M到直线l的距离是 =

所以 = ，解得b=1或b=3

因为圆心M在直线l的下方，所以b=1，

即所求圆M的方程为x2+（y﹣1）2=1

（2）解：当直线AC，BC的斜率都存在，即﹣4＜t＜﹣1时

直线AC的斜率kAC=tan2∠MAO= = ，

同理直线BC的斜率kBC=

所以直线AC的方程为y= （x﹣t），

直线BC的方程为y= （x﹣t﹣5）

解方程组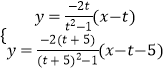

得x= ，y=

所以y= =2﹣

因为﹣4≤t≤﹣1

所以﹣ ≤t2+5t+1＜﹣3

所以 ≤y＜ ．

故当t=﹣ 时，△ABC的面积取最小值 ×5× = ．

当直线AC，BC的斜率有一个不存在时，即t=﹣4或t=﹣1时，易求得△ABC的面积为 ．

综上，当t=﹣ 时，△ABC的面积的最小值为 ．

【解析】（1）先设点M的坐标，再根据弦长可得点M到直线l的距离，进而可得b的值，从而可得圆M的方程；（2）当直线AC，BC的斜率都存在时，由已知条件可得直线AC和直线BC的方程，解方程组可得点C的坐标，进而可得△ABC面积，从而可得△ABC面积的最小值，当直线AC，BC的斜率有一个不存在时，易得△ABC面积，综上所述，可得△ABC的面积的最小值．