题目内容
【题目】如图,某公园有三条观光大道AB,BC,AC围成直角三角形,其中直角边BC=200m,斜边AB=400m,现有甲、乙、丙三位小朋友分别在AB,BC,AC大道上嬉戏,所在位置分别记为点D,E,F.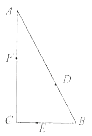
(1)若甲、乙都以每分钟100m的速度从点B出发在各自的大道上奔走,到大道的另一端时即停,乙比甲迟2分钟出发,当乙出发1分钟后,求此时甲乙两人之间的距离;
(2)设∠CEF=θ,乙丙之间的距离是甲乙之间距离的2倍,且∠DEF= ![]() ,请将甲乙之间的距离y表示为θ的函数,并求甲乙之间的最小距离.
,请将甲乙之间的距离y表示为θ的函数,并求甲乙之间的最小距离.
【答案】
(1)解:由题意,BD=300,BE=100,
△ABC中,cosB= ![]() ,B=
,B= ![]() ,
,
△BDE中,由余弦定理可得DE= ![]() =100
=100 ![]() m;
m;
(2)解:由题意,EF=2DE=2y,∠BDE=∠CEF=θ.
△CEF中,CE=EFcos∠CEF=2ycosθ
△BDE中,由正弦定理可得 ![]() =
= ![]() ,
,
∴y= ![]() =
= ![]() ,0
,0 ![]() ,
,
∴θ= ![]() ,ymin=50
,ymin=50 ![]() m.
m.
【解析】(1)先在△ABC中求出B,再在△BDE中利用余弦定理可得DE,从而可得此时甲乙两人之间的距离;(2)先在△CEF中求出CE,再在△BDE中利用正弦定理可得甲乙之间的距离y表示为θ的函数,进而利用辅助角公式和三角函数的性质可得甲乙之间的最小距离.

 快捷英语周周练系列答案
快捷英语周周练系列答案【题目】数独游戏越来越受人们喜爱,今年某地区科技馆组织数独比赛,该区甲、乙、丙、丁四所学校的学生积极参赛,参赛学生的人数如表所示:
中学 | 甲 | 乙 | 丙 | 丁 |
人数 | 30 | 40 | 20 | 10 |
为了解参赛学生的数独水平,该科技馆采用分层抽样的方法从这四所中学的参赛学生中抽取30名参加问卷调查.
(Ⅰ)问甲、乙、丙、丁四所中学各抽取多少名学生?
(Ⅱ)从参加问卷调查的30名学生中随机抽取2名,求这2名学生来自同一所中学的概率;
(Ⅲ)在参加问卷调查的30名学生中,从来自甲、丙两所中学的学生中随机抽取2名,用X表示抽得甲中学的学生人数,求X的分布列.