题目内容

8．如图，矩形长为6，宽为4，在矩形内随机地撒300颗黄豆，数得落在椭圆内的黄豆数为225颗，以此实验数据为依据可以估计出椭圆的面积约为（　　）
A．16B．17C．18D．19

分析 欲估计出椭圆的面积，可利用概率模拟，只要利用平面图形的面积比求出落在椭圆外的概率即可．

解答 解：黄豆落在椭圆外的概率为：$\frac{252}{300}=\frac{24-S}{24}$
解得：S=18．
故选：C．

点评 本题考查几何概型．如果每个事件发生的概率只与构成该事件区域的长度（面积或体积）成比例，则称这样的概率模型为几何概率模型，称为几何概型．

练习册系列答案
相关题目
18．某人射击一次，命中8-10环及不足8环的概率如下表：
命中环数不足8环8环9环10环
概率0•450•27x0•13
则此人命中环数超过8环（不含8环）的概率是0.28．
19．（本题只限理科学生做）
已知Sn为数列{an}的前n项和，且${S_n}=2{a_n}+{n^2}-3n-2$，n=1，2，3…
（Ⅰ）求证：数列{an-2n}为等比数列；
（Ⅱ）设bn=an•cosnπ，求数列{bn}的前n项和Pn；
（Ⅲ）设${c_n}=\frac{1}{{{a_n}-n}}$，数列{cn}的前n项和为Tn，求证：${T_n}＜\frac{5}{6}$．
16．已知tanα=$\frac{1}{7}$，tanβ=$\frac{1}{3}$，则tan（α+β）=（　　）
A．$\frac{1}{2}$B．$\frac{5}{11}$C．-$\frac{1}{5}$D．-$\frac{2}{11}$
3．向量$\vec a$=（x，x+2），$\vec b$=（1，2），若$\vec a∥\vec b$，则x=2；若（$\vec a-\vec b}$）⊥$\vec b$，则x=$\frac{1}{3}$．
13．执行如图所示的程序框图，若“否”箭头分别指向①和②，则输出的结果分别是（　　）
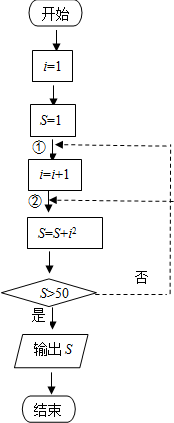
A．55，53B．51，49C．55，49D．53，51
20．已知等差数列{an}满足：a3=7，a5+a7=26．{an}的前n项和为Sn．
（Ⅰ）求an及Sn；
（Ⅱ）令bn=$\frac{4}{{{a_n}^2-1}}$（n∈N*），求数列{bn}的前n项和Tn．
17．函数f（x）=2lnx+$\frac{1}{x}$的单调递减区间是（　　）
A．（-∞，$\frac{1}{2}$]B．（0，$\frac{1}{2}$]C．[$\frac{1}{2}$，1）D．[1，+∞﹚
14．我们把形如y=f（x）φ（x）的函数称为幂指函数，幂指函数在求导时，可以利用对数法：在函数解析式两边取对数得lny=lnf（x）φ（x）=φ（x）lnf（x），两边对x求导数，得$\frac{y′}{y}$=φ′（x）lnf（x）+φ（x）$\frac{f′（x）}{f（x）}$，于是y′=f（x）φ（x）[φ′（x）lnf（x）+φ（x）$\frac{f′（x）}{f（x）}$]，运用此方法可以求得函数y=xx（x＞0）在（1，1）处的切线方程是y=x．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网