题目内容
【题目】已知抛物线![]() 上一点
上一点![]() 到其焦点
到其焦点![]() 的距离为4,椭圆
的距离为4,椭圆![]()
![]() 的离心率
的离心率![]() ,且过抛物线的焦点
,且过抛物线的焦点![]() .
.
(1)求抛物线![]() 和椭圆
和椭圆![]() 的标准方程;
的标准方程;
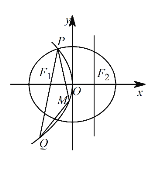
(2)过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() 两不同点,交
两不同点,交![]() 轴于点
轴于点![]() ,已知
,已知![]() ,
, ![]() ,求证:
,求证: ![]() 为定值.
为定值.
【答案】(1)抛物线的方程为![]() ,椭圆的标准方程为
,椭圆的标准方程为![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)利用抛物线C1:y2=2px上一点M(3,y0)到其焦点F的距离为4;求出p,即可得到抛物线方程,通过椭圆的离心率e=![]() ,,且过抛物线的焦点F(1,0)求出a,b,即可得到椭圆的方程;
,,且过抛物线的焦点F(1,0)求出a,b,即可得到椭圆的方程;
(2)直线l1的斜率必存在,设为k,设直线l与椭圆C2交于A(x1,y1),B(x2,y2),求出直线l的方程为y=k(x-1),N(0,-k),联立直线与椭圆的方程,利用韦达定理以及判别式,通过向量关系式即可求出λ+μ为定值.
试题解析:
(Ⅰ)抛物线的准线为![]() , 所以
, 所以![]() ,所以
,所以![]()
抛物线的方程为![]()
所以![]() ,
,![]() ,解得
,解得![]() 所以椭圆的标准方程为
所以椭圆的标准方程为![]()
(Ⅱ)直线![]() 的斜率必存在,设为
的斜率必存在,设为![]() ,设直线
,设直线![]() 与抛物线
与抛物线![]() 交于
交于![]()
则直线![]() 的方程为
的方程为![]() ,
,![]()
联立方程组:![]()
所以![]()
![]() ,
,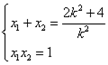 (*)
(*)
由![]() 得:
得:
![]() 得:
得:![]()
所以![]()
将(*)代入上式,得![]()

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目