题目内容
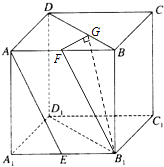
【题目】已知正方体ABCD﹣A1B1C1D1中,点E是棱A1B1的中点,则直线AE与平面BDD1B1所成角的正弦值 . 
【答案】![]()
【解析】解:取AB的中点F,连接B1F,过点F作FG⊥BD,垂足为G,连接B1G,
由正方体性质易知BB1⊥平面ABCD,又FG平面ABCD,
∴BB1⊥FG
又FG⊥BD,BD∩BB1=B,BD平面BDD1B1 , BB1平面BDD1B1
∴FG⊥平面BDD1B1
∴∠FB1G为B1F与平面平面BDD1B1所成角
设正方体ABCD﹣A1B1C1D1棱长为1,
∴FG= ![]() ,B1F=
,B1F= ![]()
∴sin∠B1FO= 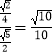
而AE∥B1F,所以直线AE与平面BDD1B1所成角的正弦值为 ![]()
所以答案是: ![]()
【考点精析】本题主要考查了空间角的异面直线所成的角的相关知识点,需要掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则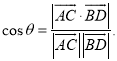 才能正确解答此题.
才能正确解答此题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目