题目内容
5. 设△ABC三个内角A、B、C所对的边分别为a,b,c.已知C=$\frac{π}{3}$,acosA=bcosB.
设△ABC三个内角A、B、C所对的边分别为a,b,c.已知C=$\frac{π}{3}$,acosA=bcosB.(1)求角B的大小;
(2)如图,在△ABC内取一点P,使得PB=2.过点P分别作直线BA、BC的垂线PM、PN,垂足分别是M、N.设∠PBA=α,求PM+PN的最大值及此时α的取值.
分析 (1)由acosA=bcosB及正弦定理可得:sinAcosA=sinBcosB,即sin2A=sin2B,又A∈(0,π),B∈(0,π),可得A=B或A+B=$\frac{π}{2}$. 由于C=$\frac{π}{3}$,即可得出.
(2)由题设,得在Rt△PMB中,PM=PB•sin∠PBM=2sinα;在Rt△PNB中,同理可得PN=2sin($\frac{π}{3}$-α),α∈(0,$\frac{π}{3}$).于是PM+PN=2sin(α+$\frac{π}{3}$).由于α∈(0,$\frac{π}{3}$),可得sin(α+$\frac{π}{3}$)∈($\frac{\sqrt{3}}{2}$,1],即可得出.
解答 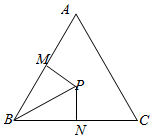 解:(1)由acosA=bcosB及正弦定理可得:sinAcosA=sinBcosB,
解:(1)由acosA=bcosB及正弦定理可得:sinAcosA=sinBcosB,
即sin2A=sin2B,又A∈(0,π),B∈(0,π),
∴有A=B或A+B=$\frac{π}{2}$.
又∵C=$\frac{π}{3}$,得A+B=$\frac{2π}{3}$,与A+B=$\frac{π}{2}$矛盾,
∴A=B,因此B=$\frac{π}{3}$.
(2)由题设,得在Rt△PMB中,PM=PB•sin∠PBM=2sinα;
在Rt△PNB中,PN=PB•sin∠PBN=PB•sin($\frac{π}{3}$-∠PBA)=2sin($\frac{π}{3}$-α),α∈(0,$\frac{π}{3}$).
∴PM+PN=2sinα+2sin($\frac{π}{3}$-α)=sinα+$\sqrt{3}$cosα=2sin(α+$\frac{π}{3}$).
∵α∈(0,$\frac{π}{3}$),∴α+$\frac{π}{3}$∈($\frac{π}{3}$,$\frac{2π}{3}$),从而有sin(α+$\frac{π}{3}$)∈($\frac{\sqrt{3}}{2}$,1],
即2sin(α+$\frac{π}{3}$)∈($\sqrt{3}$,2].
于是,当α+$\frac{π}{3}$=$\frac{π}{2}$,即α=$\frac{π}{6}$时,PM+PN取得最大值2.
点评 本题查克拉正弦定理、倍角公式、和差公式、三角函数的单调性,考查了推理能力与计算能力,属于中档题.

 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案| A. | $\frac{4}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{2}{5}$ |
| A. | [-2,0) | B. | [-2,+∞) | C. | (-2,0) | D. | (-∞,2] |
| 项目方式 | 基本费 | 网络使用费 | 通信费 |
| 963 | 0 | 0.05元/min | 0.02元/min |
| 169 | 100元/月 | 1元/h |
(1)若某用户以“963”方式上网,上网多长时间,网络使用费达到100元;
(2)分别写出以“963”方式和“169”方式上网的月上网费y(元)与月上网时间t(h)之间的函数关系式;
(3)若某用户平均每月上网时间为120h,试问他用哪种方式上网合算.