题目内容
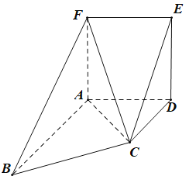
【题目】已知棱长为1的正方体![]() ,点
,点![]() 是四边形
是四边形![]() 内(含边界)任意一点,
内(含边界)任意一点,![]() 是
是![]() 中点,有下列四个结论:
中点,有下列四个结论:
①![]() ;②当
;②当![]() 点为
点为![]() 中点时,二面角
中点时,二面角![]() 的余弦值
的余弦值![]() ;③
;③![]() 与
与![]() 所成角的正切值为
所成角的正切值为![]() ;④当
;④当![]() 时,点
时,点![]() 的轨迹长为
的轨迹长为![]() .
.
其中所有正确的结论序号是( )
A.①②③B.①③④C.②③④D.①②④
【答案】B
【解析】
①利用线面平行,得到线线平行。②要求二面角的余弦值,转化为求二面角的平面角余弦值。③要求线线角,将其平移至一个三角形中,即可求解。④证明![]() 平面
平面![]() ,则
,则![]() 即为点
即为点![]() 的运动路径,通过计算即可求解。
的运动路径,通过计算即可求解。
解:如图所示,

①根据正方体的几何性质,易得![]() 平面
平面![]() ,又因为
,又因为![]() 平面
平面![]() , 故
, 故![]() ,即
,即![]() ,故①对。
,故①对。
②当![]() 点为
点为![]() 中点时,
中点时,![]() ,且
,且![]() ,所以二面角
,所以二面角![]() 的平面角为
的平面角为![]() ,连接
,连接![]() ,又
,又![]() ,故所求二面角的余弦值为
,故所求二面角的余弦值为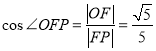 .故②错。
.故②错。
③因为![]() ,所以
,所以![]() 与
与![]() 所成角即为
所成角即为![]() 与
与![]() 所成角,即为
所成角,即为![]() ,连接
,连接![]() ,在等腰三角形
,在等腰三角形![]() 中,
中,![]() 为底边中点,所以
为底边中点,所以![]() ,所以
,所以![]() 与
与![]() 所成角的正切值为
所成角的正切值为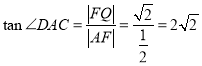 .故③对。
.故③对。
④点![]() 为
为![]() 中点,所以
中点,所以![]() ,又因为
,又因为![]() 所以
所以![]() 平面
平面![]() , 即点
, 即点![]() 在线段
在线段![]() 上运动时,
上运动时,![]() ,所以点
,所以点![]() 的轨迹长为
的轨迹长为![]() ,故④对。
,故④对。
故选![]() .
.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目