题目内容
【题目】已知点A，B是抛物线
上关于轴对称的两点，点E是抛物线C的准线与x轴的交点.
（1）若
是面积为4的直角三角形，求抛物线C的方程；
（2）若直线BE与抛物线C交于另一点D，证明：直线AD过定点.
【答案】(1) 
；(2) 证明见解析
【解析】
（1）根据直角三角形的性质，可以得到
三点在以焦点为圆心，
为半径的圆上，故点
，
,
,再根据三角形面积，即可求出。
（2）设
,
所在直线方程和抛物线方程，通过韦达定理，得到斜率的表达式，进而得到
所在直线的表达式，通过化简整理，即可证明。
解：（1）由题意，
是等腰直角三角形，且
不妨设点A位于第一象限，则直线EA的方程为
，
联立方程，
，解得
所以点
，
，
，解得
，
故抛物线C的方程为
（2）（方法一）设
，
，则直线EB的方程为
联立方程，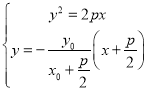
，消去
，
得关于
的方程
该方程有一个根
，两根之积为
，
则另一个根为
，所以点D的坐标为
直线AD的斜率为
所以AD的方程为
化简得
所以直线AD过定点
（方法二）设
，
，
，直线BE的方程为
，
联立方程，
，消去x，
得关于x的方程
，所以
则
直线AD的方程为
化简得
所以直线AD过定点
练习册系列答案
阅读快车系列答案
相关题目
