题目内容
【题目】如图,在三棱锥![]() 中,N为CD的中点,M是AC上一点.
中,N为CD的中点,M是AC上一点.
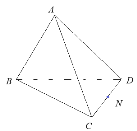
(1)若M为AC的中点,求证:AD//平面BMN;
(2)若![]() ,平面
,平面![]() 平面BCD,
平面BCD,![]() ,求直线AC与平面BMN所成的角的余弦值。
,求直线AC与平面BMN所成的角的余弦值。
【答案】(1)详见解析(2)![]()
【解析】
(1)由![]() ,即可证明出AD//平面BMN;
,即可证明出AD//平面BMN;
(2)向量法,建立空间直角坐标系,求出![]() 以及面BMN的法相量
以及面BMN的法相量![]() ,利用直线AC与平面BMN所成的角为
,利用直线AC与平面BMN所成的角为![]() ,则
,则![]() 即可求出AC与平面BMN所成的角的正弦值,进而求出余弦值。
即可求出AC与平面BMN所成的角的正弦值,进而求出余弦值。
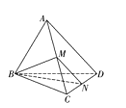
(1)证明:如图,在![]() 中,因为M,N分别为棱AC,CD的中点,连接MN,
中,因为M,N分别为棱AC,CD的中点,连接MN,
所以![]() ,又
,又![]() 平面BMN,
平面BMN,![]() 平面BMN,
平面BMN,
所以![]() 平面BMN
平面BMN
(2)解:取BD的中点O,连接AO,因为![]() ,所以
,所以![]() ,又因为平面
,又因为平面![]() 平面BCD,平面
平面BCD,平面![]() 平面BCD=BD,
平面BCD=BD,![]() ,
,![]() 平面ABO,
平面ABO,
所以![]() 平面BCD,所以
平面BCD,所以![]() .
.
又![]() ,
,![]() 平面ABO
平面ABO
所以![]() 平面ABO,
平面ABO,
![]() 平面ABO,所以
平面ABO,所以![]()
连接ON,所以![]() ,所以
,所以![]() ,
,
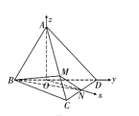
如图建系,
设![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]() ,
,
![]()
所以![]() ,则
,则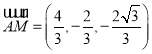
所以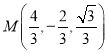 ,则
,则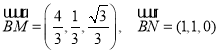
设平面BMN的一个法向量为![]() ,
,
则 ,即
,即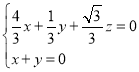
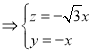
令![]() ,则
,则![]()
设直线AC与平面BMN所成的角为![]() ,
,
则![]()
又![]() ,所以
,所以![]() ,
,
所以直线AC与平面BMN所成的角的余弦值为![]()

 轻松夺冠全能掌控卷系列答案
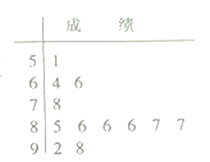
轻松夺冠全能掌控卷系列答案【题目】某企业为了检查生产![]() 产品的甲、乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在
产品的甲、乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.下表是甲流水线样本的频数分布表,下图是乙流水线样本的频率分布直方图.
内,则为合格品,否则为不合格品.下表是甲流水线样本的频数分布表,下图是乙流水线样本的频率分布直方图.
甲流水线样本的频数分布表
质量指标值 | 频数 |
| 9 |
| 10 |
| 17 |
| 8 |
| 6 |
乙流水线样本的频率分布直方图
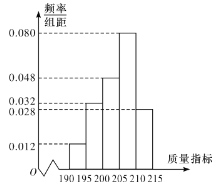
(1)根据图形,估计乙流水线生产的![]() 产品的该项质量指标值的中位数;
产品的该项质量指标值的中位数;
(2)设该企业生产一件合格品获利100元,生产一件不合格品亏损50元,若某个月内甲、乙两条流水线均生产了1000件产品,若将频率视为概率,则该企业本月的利润约为多少元?
【题目】一商场对每天进店人数和商品销售件数进行了统计对比,得到如下表格:
人数 | 10 | 15 | 20 | 25 | 30 | 35 | 40 |
件数 | 4 | 7 | 12 | 15 | 20 | 23 | 27 |
(1)在答题卡给定的坐标系中画出表中数据的散点图,并由散点图判断销售件数![]() 与进店人数
与进店人数![]() 是否线性相关?(给出判断即可,不必说明理由);
是否线性相关?(给出判断即可,不必说明理由);
(2)建立![]() 关于
关于![]() 的回归方程(系数精确到0.01),预测进店人数为80时,商品销售的件数(结果保留整数).
的回归方程(系数精确到0.01),预测进店人数为80时,商品销售的件数(结果保留整数).
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
参考公式: ,
,![]() ,其中
,其中![]() ,
,![]() 为数据
为数据![]() 的平均数.
的平均数.