Question

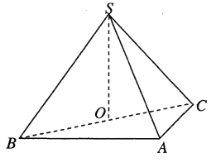
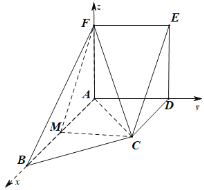
【题目】如图所示的几何体中，正方形与梯形所在的平面互相垂直，， ，，.

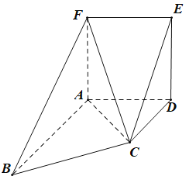
（1）求证:平面；

（2）求证:平面平面；

（3）求二面角的余弦值.

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）.

【解析】

（1）取AB中点M，连结MF，MC，可证四边形MCEF为平行四边形，得EC∥MF，进而得证；

（2）由题干面面垂直的性质可得，平面ADEF∩平面ABCD=AD，又AF⊥AD，可证AF⊥平面ABCD，进而得证；

（3）以A为原点，AB，AD，AF所在直线分别为x，y，z轴，建立空间直角坐标系，求出对应的点坐标，表示出向量，分别求出平面ABF和平面BCF的法向量，结合向量夹角公式即可求解

（1）取AB中点M，连结MF，MC，∵MACD，且MACD，∴四边形MCEF为平行四边形，∴EC∥MF，∵EC平面ABF，MF平面ABF，∴EC∥平面ABF.

（2）∵平面ADEF⊥平面ABCD，平面ADEF∩平面ABCD=AD， AF⊥AD，AF平面ADEF，∴AF⊥平面ABCD，又∵AF平面FAC，∴平面FAC⊥平面ABCD.

（3)以A为原点，AB，AD，AF所在直线分别为x，y，z轴，建立空间直角坐标系，

则B(4，0，0)，F(0，0，2)，C(2，2，0)，(﹣2，2，0)，(﹣4，2，0)，平面ABF的一个法向量(0，1，0)，设平面BCF的法向量(x，y，z)，则，取x=1，得(1，1，2)，设二面角A﹣BF﹣C的平面角为θ，则cosθ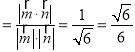.∴二面角A﹣BF﹣C的余弦值为.