题目内容
【题目】2019年是新中国成立七十周年，新中国成立以来，我国文化事业得到了充分发展，尤其是党的十八大以来，文化事业发展更加迅速，下图是从2013 年到 2018 年六年间我国公共图书馆业机构数（个）与对应年份编号的散点图（为便于计算，将 2013 年编号为 1，2014 年编号为 2，…，2018年编号为 6，把每年的公共图书馆业机构个数作为因变量，把年份编号从 1 到 6 作为自变量进行回归分析），得到回归直线
，其相关指数
，给出下列结论，其中正确的个数是( )
①公共图书馆业机构数与年份的正相关性较强
②公共图书馆业机构数平均每年增加13.743个
③可预测 2019 年公共图书馆业机构数约为3192个
A.0B.1C.2D.3
【答案】D
【解析】
根据
和
确定是正相关还是负相关以及相关性的强弱；根据的值判断平均每年增加量；根据回归直线方程预测
年公共图书馆业机构数.
由图知点散布在从左下角到右上角的区域内，所以为正相关，
又
趋近于1，所以相关性较强，故①正确；由回归方程知②正确；
由回归方程，当
时，得估计值为3191.9≈3192，故③正确.
故选：D.
【题目】某省即将实行新高考，不再实行文理分科.某校研究数学成绩优秀是否对选择物理有影响，对该校2018级的500名学生进行调在收集到相关数据如下：
选物理 | 不选物理 | 总计 | |
数学成绩优秀 | |||
数学成绩不优秀 | 130 | ||
总计 | 300 | 500 |
（1）根据以上提供的信息，完成
列联表，并完善等高条形图；
（2）能否在犯错误的概率不超过0.05的前提下认为数学成绩优秀与选物理有关？
附：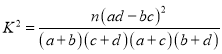
.
临界值表：
P（ | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
【题目】假设关于某设备的使用年限x（年）和所支出的维修费用y万元有如下的统计资料：
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
（1）画出散点图并判断是否线性相关；
（2）如果线性相关，求线性回归方程；
（3）估计使用年限为10年时，维修费用是多少？
附注：①参考公式：回归方程
中斜率和截距的最小二乘估计分别为
；
②参考数据：
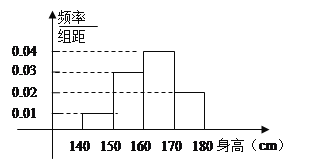
【题目】某网购平台为了解某市居民在该平台的消费情况，从该市使用其平台且每周平均消费额超过100元的人员中随机抽取了100名，并绘制如图所示频率分布直方图，已知中间三组的人数可构成等差数列.
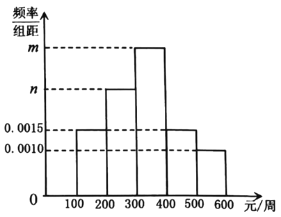
（1）求
的值；
（2）分析人员对100名调查对象的性别进行统计发现，消费金额不低于300元的男性有20人，低于300元的男性有25人，根据统计数据完成下列
列联表，并判断是否有
的把握认为消费金额与性别有关？
（3）分析人员对抽取对象每周的消费金额
与年龄
进一步分析，发现他们线性相关，得到回归方程
.已知100名使用者的平均年龄为38岁，试判断一名年龄为25岁的年轻人每周的平均消费金额为多少.（同一组数据用该区间的中点值代替）
列联表
男性 | 女性 | 合计 | |
消费金额 | |||
消费金额 | |||
合计 |
临界值表：
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
，其中
