题目内容
若一个正方体的表面积为S1，其外接球的表面积为S2，则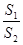
＝________.
＝________.
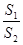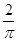
设正方体棱长为a，则正方体表面积为S1＝6a2，其外接球半径为正方体体对角线长的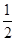
，即为
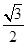a，因此外接球的表面积为S2＝4πr2＝3πa2，则＝
＝.
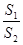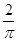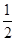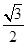，即为a，因此外接球的表面积为S2＝4πr2＝3πa2，则＝＝.
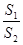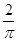练习册系列答案
相关题目
题目内容
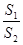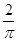
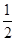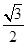＝________.，即为a，因此外接球的表面积为S2＝4πr2＝3πa2，则＝＝.
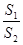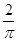中，底面
是边长为
的正方形，侧棱
底面
，
是
的中点．
平面
；
的体积．
中，底面ABCD和侧面
都是矩形，E是CD的中点，
，
.
；
，求三棱锥
的体积.
的棱长为2，E、F分别是
、
的中点，过
、E、F作平面
交
于G．
；
的余弦值；
的体积．
的正三棱锥
中，
长为
，
为棱
的中点，求
与
所成角的大小（结果用反三角函数值表示）；
π
.
中侧棱垂直于底面，
，
，
，且三棱柱