题目内容
(满分16分)
已知函数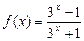 (
(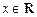 ).
).
(1)求函数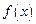 的值域;
的值域;
(2)判断函数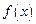 的奇偶性;
的奇偶性;
(3)用定义判断函数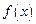 的单调性;
的单调性;
(4)解不等式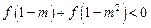
(1)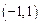
(2)奇函数,证明略
(3)函数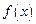 在
在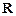 上为单调增函数
上为单调增函数
(4)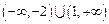
解析(1)∵ 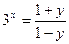 ,………………………… 2分
,………………………… 2分
又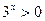 ,∴
,∴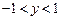
∴函数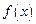 的值域为
的值域为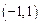 ………………………………4分
………………………………4分
(2)证明:①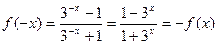 , ………………………6分
, ………………………6分
∴函数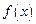 为奇函数 ………………………8分
为奇函数 ………………………8分
(3) 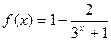
在定义域中任取两个实数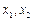 ,且
,且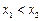 , …………………………9分
, …………………………9分
则 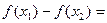
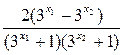 …………………………10分
…………………………10分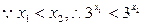 ,从而
,从而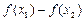
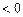 …………………………11分
…………………………11分
∴函数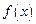 在
在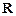 上为单调增函数 …………………………12分
上为单调增函数 …………………………12分
(4)由(2)得函数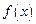 为奇函数,在R上为单调增函数
为奇函数,在R上为单调增函数
∴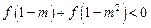 即
即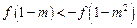 ,
,
∴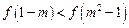 ,
,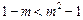 …………………………14分
…………………………14分
∴原不等式的解集为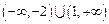 …………………………16分
…………………………16分

练习册系列答案
相关题目
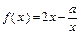 的定义域为(0,1](
的定义域为(0,1](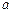 为实数).
为实数).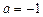 时,求函数
时,求函数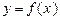 的值域;
的值域;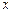 的值
的值 R,m,n都是不为1的正数,函数
R,m,n都是不为1的正数,函数
 ,请判断函数
,请判断函数 是否具有奇偶性. 如果具有,求出相
是否具有奇偶性. 如果具有,求出相 ,且
,且 ,请判断函数
,请判断函数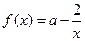 .
. 的奇偶性;
的奇偶性; 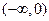 上的单调性并用定义证明.
上的单调性并用定义证明. (微克)与服药后的时间
(微克)与服药后的时间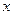 (小时)之间近似满足如图所示的曲线,其中OA 是线段,曲线 ABC 是函数
(小时)之间近似满足如图所示的曲线,其中OA 是线段,曲线 ABC 是函数 (
( )的图象,且
)的图象,且 是常数.
是常数.
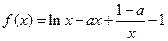
 .
.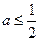 时,讨论
时,讨论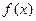 的单调性;
的单调性;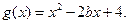 当
当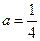 时,若对任意
时,若对任意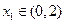 ,存在
,存在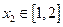 ,使
,使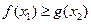 恒成立,求实数
恒成立,求实数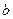 取值范围.
取值范围.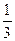
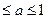 , 若
, 若 在区间
在区间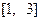 上的最大值为
上的最大值为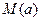 , 最小值为
, 最小值为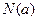 , 令
, 令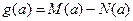 .
.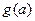 的函数表达式;
的函数表达式; +ax
+ax +bx+c的图像,如图所示,且与y=0在原点相切,若函数的极小值为–4,
+bx+c的图像,如图所示,且与y=0在原点相切,若函数的极小值为–4,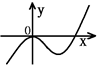
 在
在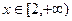 上是增函数;
上是增函数; 在
在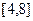 上的值域。
上的值域。