题目内容
【题目】有一座大桥既是交通拥挤地段，又是事故多发地段，为了保证安全，交通部门规定：大桥上的车距
与车速
和车长
的关系满足
为正的常数)．假定车身长为
，当车速为
时，车距为
个车身长．
（1）写出车距关于车速的函数关系式；
（2）应规定怎样的车速，才能使大桥上每小时通过的车辆最多？
【答案】（1）d＝0．0024v2＋2；（2）当车速为50 km/h时，大桥上每小时通过的车辆最多.
【解析】试题分析：（1）根据当车速
，车距为
个车身长，建立等式关系，求出
的值，即可求出车距
关于车速
的函数关系式；（2）设每小时通过的车辆为
，每小时内通过汽车的数量为最大，只须
最小，将 代入，然后利用基本求出最值，即可求出所求.
试题解析：（1） 由题意，当v＝60时，d＝2．66l，
所以k＝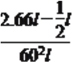
＝
＝0．0006，
所以d＝0．0024v2＋2．
（2）设每小时通过的车辆数为Q，则Q＝
．
即Q＝
＝
．
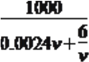因为0．0024v＋
≥2
＝0．24，
所以Q≤
＝
，当且仅当0．0024v＝，即v＝50时，Q取最大值．
故当车速为50 km/h时，大桥上每小时通过的车辆最多．
【题目】某公司计划在今年内同时出售变频空调机和智能洗衣机，由于这两种产品的市场需求量非常大，有多少就能销售多少，因此该公司要根据实际情况(如资金、劳动力)确定产品的月供应量，以使得总利润达到最大.已知对这两种产品有直接限制的因素是资金和劳动力，经调查，得到关于这两种产品的有关数据如下表：
资金 | 每台产品所需资金（百元） | 月资金供应量 （百元） | |
空调机 | 洗衣机 | ||
成本 | 30 | 20 | 300 |
劳动力（工资） | 5 | 10 | 110 |
每台产品利润 | 6 | 8 | |
试问：怎样确定两种货物的月供应量，才能使总利润最大？最大利润是多少?
【题目】（本小题满分14分）体育测试成绩分为四个等级：优、良、中、不及格．某班50名学生参加测试的结果如下：
等级 | 优 | 良 | 中 | 不及格 |
人数 | 5 | 19 | 23 | 3 |
（1）从该班任意抽取1名学生，求这名学生的测试成绩为“良”或“中”的概率；
（2）测试成绩为“优”的3名男生记为
，
，
，2名女生记为
，
．现从这5人中任选2人参加学校的某项体育比赛．
① 写出所有等可能的基本事件；
② 求参赛学生中恰有1名女生的概率．
【题目】为了普及法律知识，达到“法在心中”的目的，某市法制办组织了普法知识竞赛．统计局调查队随机抽取了甲、乙两单位中各5名职工的成绩，成绩如下表：
甲单位 | 87 | 88 | 91 | 91 | 93 |
乙单位 | 85 | 89 | 91 | 92 | 93 |
（1）根据表中的数据，分别求出甲、乙两单位职工成绩的平均数和方差，并判断哪个单位对法律知识的掌握更稳定；
（2）用简单随机抽样法从乙单位5名职工中抽取2名，他们的成绩组成一个样本，求抽取的2名职工的分数差至少是4的概率．
