题目内容
【题目】心理学家发现,学生的接受能力依赖于老师引入概念和描述问题所用的时间,上课开始时,学生的兴趣激增,中间有一段不太长的时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,并趋于稳定.分析结果和实验表明,设提出和讲述概念的时间为![]() (单位:分),学生的接受能力为
(单位:分),学生的接受能力为![]() (
(![]() 值越大,表示接受能力越强),
值越大,表示接受能力越强),
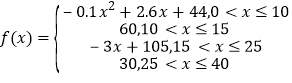
(1)开讲后多少分钟,学生的接受能力最强?能维持多少时间?
(2)试比较开讲后5分钟、20分钟、35分钟,学生的接受能力的大小;(3)若一个数学难题,需要56的接受能力以及12分钟时间,老师能否及时在学生一直达到所需接受能力的状态下讲述完这个难题?
【答案】(1)开讲后10分钟,学生的接受能力最强,并能维持5分钟.(2)从大小依次是开讲后5分钟、20分钟、35分钟的接受能力(3)不能
【解析】试题分析:(1)求学生的接受能力最强其实就是要求分段函数的最大值,方法是分别求出各段的最大值取其最大即可;(2)比较![]() 分钟、
分钟、![]() 分钟、
分钟、![]() 分钟学生的接受能力大小,方法是把
分钟学生的接受能力大小,方法是把![]() 代入第一段函数中,而
代入第一段函数中,而![]() 要代入到第三段函数中,
要代入到第三段函数中,![]() 代入第四段函数,比较大小即可;(3)在每一段上解不等式
代入第四段函数,比较大小即可;(3)在每一段上解不等式![]() ,求出满足条件的
,求出满足条件的![]() ,从而得到接受能力
,从而得到接受能力![]() 及以上的时间,然后与
及以上的时间,然后与![]() 进行比较即可.
进行比较即可.
试题解析:(Ⅰ)由题意可知:
![]()
所以当X=10时, ![]() 的最大值是60,
的最大值是60,
又![]() ,
, ![]() =60
=60
所以开讲后10分钟,学生的接受能力最强,并能维持5分钟.
(Ⅱ)由题意可知:![]()
所以开讲后5分钟、20分钟、35分钟的学生的接受能力从大小依次是
开讲后5分钟、20分钟、35分钟的接受能力;
(Ⅲ)由题意可知:
当 ![]()
解得:![]()
当![]()
![]() =60>56,满足要求;
=60>56,满足要求;
当![]() ,
,![]()
解得:![]()
因此接受能力56及以上的时间是![]() 分钟小于12分钟.
分钟小于12分钟.
所以老师不能在所需的接受能力和时间状态下讲述完这个难题 .

练习册系列答案
相关题目