Question

【题目】（本小题满分14分）

在四棱锥P－ABCD中，BC∥AD，PA⊥PD，AD＝2BC，AB＝PB， E为PA的中点．

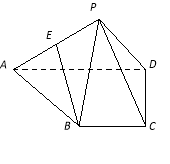
（1）求证：BE∥平面PCD；

（2）求证：平面PAB⊥平面PCD．

Answer 1

【答案】证明见解析.

【解析】

试题分析：（1）要证明BE∥平面PCD，就是要在平面PCD上找到一条与BE平行的直线，由判定定理，从已知，又是中点，因此我们取中点，可得，且，从而有且，于是是平行四边形，，平行线找到了；（2）要证明平面PAB⊥平面PCD，而题中已知PA⊥PD，由面面垂直的性质，中一定有一条直线与其中一个平面垂直，由已知，因此，再由（1），这样结合就有，于是有面面垂直.

试题解析：（1）取PD的中点F，连接EF，CF．

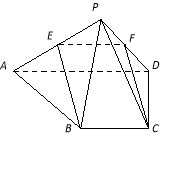
因为E为PA的中点，所以EF∥AD，EF＝AD．

因为BC∥AD，BC＝AD，

所以EF∥BC，EF＝BC．

所以四边形BCFE为平行四边形．

所以BE∥CF． 4分

因为BE平面PCD，CF平面PCD，

所以BE∥平面PCD． 6分

（2）因为AB＝PB，E为PA的中点，所以PA⊥BE．

因为BE∥CF，所以PA⊥CF． 9分

因为PA⊥PD，PD平面PCD，CF平面PCD，PD∩CF＝F，

所以PA⊥平面PCD． 12分

因为PA平面PAB，所以平面PAB平面PCD． 14分