Question

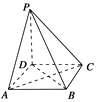
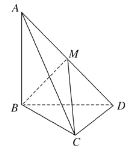
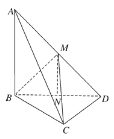
【题目】如图，三棱锥A－BCD中，AB⊥平面BCD，CD⊥BD .

（1）求证：CD⊥平面ABD；

（2）若AB＝BD＝CD＝1，M为AD中点，求三棱锥A－MBC的体积．

Answer 1

【答案】（1）详见解析（2）

【解析】

试题分析：（Ⅰ）证明：CD⊥平面ABD，只需证明AB⊥CD；（Ⅱ）利用转换底面，VA-MBC=VC-ABM=S△ABMCD，即可求出三棱锥A-MBC的体积

试题解析：（1）∵AB⊥平面BCD，CD平面BCD，

∴AB⊥CD.

又∵CD⊥BD，AB∩BD＝B，

AB平面ABD，BD平面ABD，

∴CD⊥平面ABD.

（2）法一：由AB⊥平面BCD，得AB⊥BD，

∵AB＝BD＝1，∴S△ABD＝.

∵M是AD的中点，

∴S△ABM＝S△ABD＝

由（1）知，CD⊥平面ABD，

∴三棱锥C－ABM的高h＝CD＝1，

因此三棱锥A－MBC的体积

VA－MBC＝VC－ABM＝S△ABM·h＝.

法二：由AB⊥平面BCD知，平面ABD⊥平面BCD，又平面ABD∩平面BCD＝BD，如图，过点M作MN⊥BD交BD于点N，则MN⊥平面BCD，且MN＝AB＝，又CD⊥BD，BD＝CD＝1，

∴S△BCD＝.

∴三棱锥A－MBC的体积

VA－MBC＝VA－BCD－VM－BCD

＝AB·S△BCD－MN·S△BCD

＝.