题目内容
【题目】已知函数f（x）=cos（ωx+ 
），（ω＞0，0＜φ＜π），其中x∈R且图象相邻两对称轴之间的距离为 
；
（1）求f（x）的对称轴方程和单调递增区间；
（2）求f（x）的最大值、最小值，并指出f（x）取得最大值、最小值时所对应的x的集合．
【答案】
（1）解：函数f（x）=cos（ωx+ 
）的图象的两对称轴之间的距离为 
= 
，
∴ω=2，f（x）=cos（2x+ ）．
令2x+ =kπ，求得x= 
﹣ 
，可得对称轴方程为 x= ﹣ ，k∈Z．
令2kπ﹣π≤2x+ ≤2kπ，求得 kπ﹣ 
≤x≤kπ﹣ ，
可得函数的增区间为[kπ﹣ ，kπ﹣ ]，k∈Z
（2）解：当2x+ =2kπ，即x=kπ﹣ ，k∈Z时，f（x）取得最大值为1．
当2x+ =2kπ+π，即x=kπ+ ，k∈Z时，f（x）取得最小值为﹣1．
∴f（x）取最大值时相应的x集合为{x|x=kπ﹣ ，k∈Z}；
f（x）取最小值时相应的x集合为{x|x=kπ+ ，k∈Z}
【解析】（1）由条件利用余弦函数的图象特征，求得ω的值，可得函数的解析式，再利用余弦函数的单调性得出结论．（2）由条件利用余弦函数的最值，求得f（x）取得最大值、最小值时所对应的x的集合．
【题目】某公司对新研发的一种产品进行合理定价，且销量与单价具有相关关系，将该产品按事先拟定的价格进行试销，得到如下数据：
单价x（单位：元） | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量y（单位：万件） | 90 | 84 | 83 | 80 | 75 | 68 |
（1）现有三条y对x的回归直线方程： 
=﹣10x+170； =﹣20x+250； =﹣15x+210；根据所学的统计学知识，选择一条合理的回归直线，并说明理由．
（2）预计在今后的销售中，销量与单价服从（1）中选出的回归直线方程，且该产品的成本是每件5元，为使公司获得最大利润，该产品的单价应定多少元？（利润=销售收入﹣成本）
【题目】在物理实验中，为了研究所挂物体的重量x对弹簧长度y的影响．某学生通过实验测量得到物体的重量与弹簧长度的对比表：
物体重量（单位g） | 1 | 2 | 3 | 4 | 5 |
弹簧长度（单位cm） | 1.5 | 3 | 4 | 5 | 6.5 |
参考公式：
①．样本数据x1 ， x2 ， …xn的标准差
s= 
，其中 
为样本的平均数；
②．线性回归方程系数公式 
= 
= 
， 
= 
﹣ ．
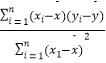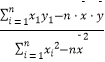（1）画出散点图；
（2）利用所给的参考公式，求y对x的回归直线方程；
（3）预测所挂物体重量为8g时的弹簧长度．
