题目内容
【题目】已知函数f(x)=cosωxsin(ωx﹣ ![]() )+
)+ ![]() cos2ωx﹣
cos2ωx﹣ ![]() (ω>0,x∈R),且函数y=f(x)图象的一个对称中心到它对称轴的最近距离为
(ω>0,x∈R),且函数y=f(x)图象的一个对称中心到它对称轴的最近距离为 ![]() .
.
(1)求ω的值及f(x)的对称轴方程;
(2)在△ABC中,角A,B,C的对边分别为a,b,c,若f(A)=0,sinB= ![]() ,a=
,a= ![]() ,求b的值.
,求b的值.
【答案】
(1)解:函数f(x)=cosωxsin(ωx﹣ ![]() )+
)+ ![]() cos2ωx﹣
cos2ωx﹣ ![]() (ω>0,x∈R),
(ω>0,x∈R),
化简可得:f(x)= ![]() sinωxcosωx﹣
sinωxcosωx﹣ ![]() cos2ωx+
cos2ωx+ ![]() cos2ωx﹣
cos2ωx﹣ ![]() (ω>0,x∈R),
(ω>0,x∈R),
= ![]() sin2ωx+
sin2ωx+ ![]() cos2ωx﹣
cos2ωx﹣ ![]() =
= ![]() sin2ωx+
sin2ωx+ ![]() cos2ωx=
cos2ωx= ![]() sin(2ωx
sin(2ωx ![]() )
)
∵函数y=f(x)图象的一个对称中心到它对称轴的最近距离为 ![]() .
.
∴T=4× ![]() =π,
=π,
∴ ![]() ,
,
故得ω=1.
∴f(x)= ![]() sin(2x
sin(2x ![]() ),
),
对称轴方程:2x ![]() =
= ![]() ,
,
得:x= ![]() ,k∈Z.
,k∈Z.
∴f(x)的对称轴方程为:x= ![]() ,k∈Z.
,k∈Z.
(2)解:∵f(A)=0,即sin(2A ![]() )=0,
)=0,
∴2A ![]() =kπ,
=kπ,
∵0<A<π,
∴A= ![]() ,
,
∵sinB= ![]() ,a=
,a= ![]() ,
,
由正弦定理, ![]() ,可得:
,可得: ![]() ,解得:b=
,解得:b= ![]() .
.
故得b的值为: ![]() .
.
【解析】(1)利用二倍角和两角和与差以及辅助角公式基本公式将函数化为y=Asin(ωx+φ)的形式,对称中心到它对称轴的最近距离为 ![]() ,可得周期T,从而求出ω.结合三角函数的图象和性质,可得f(x)的对称轴方程;(2)根据f(A)=0,求解出A角的大小,sinB=
,可得周期T,从而求出ω.结合三角函数的图象和性质,可得f(x)的对称轴方程;(2)根据f(A)=0,求解出A角的大小,sinB= ![]() ,a=
,a= ![]() ,根据正弦定理可得b的值.
,根据正弦定理可得b的值.

 53天天练系列答案
53天天练系列答案【题目】调查某车间20名工人的年龄,第i名工人的年龄为ai,具体数据见表:
i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
ai | 29 | 28 | 30 | 19 | 31 | 28 | 30 | 28 | 32 | 31 | 30 | 31 | 29 | 29 | 31 | 32 | 40 | 30 | 32 | 30 |
(1)作出这20名工人年龄的茎叶图;
(2)求这20名工人年龄的众数和极差;
(3)执行如图所示的算法流程图(其中 ![]() 是这20名工人年龄的平均数),求输出的S值.
是这20名工人年龄的平均数),求输出的S值. 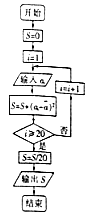
【题目】某网站对“爱飞客”飞行大会的日关注量x(万人)与日点赞量y(万次)进行了统计对比,得到表格如下:
x | 3 | 5 | 6 | 7 | 9 |
y | 2 | 3 | 3 | 4 | 5 |
由散点图象知,可以用回归直线方程 ![]() 来近似刻画它们之间的关系.
来近似刻画它们之间的关系.
(Ⅰ)求出y关于x的回归直线方程,并预测日关注量为10万人时的日点赞量;
(Ⅱ)一个三口之家参加“爱飞客”亲子游戏,游戏规定:三人依次从装有3个白球和2个红球的箱子中不放回地各摸出一个球,大人摸出每个红球得奖金10元,小孩摸出1个红球得奖金50元.求该三口之家所得奖金总额不低于50元的概率.
参考公式:b= 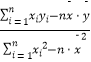 ; 参考数据:
; 参考数据: ![]() =200,
=200, ![]() =112.
=112.
