题目内容
15.已知数列{an}、{bn},且通项公式分别为an=3n-2,bn=n2,现抽出数列{an}、{bn}中所有相同的项并按从小到大的顺序排列成一个新的数列{cn},则c10=196(填数字).分析 由an=3n-2,bn=n2,分别得出:此两个数列所有的项按从小到大的顺序排列.现抽出数列{an}、{bn}中所有相同的项并按从小到大的顺序排列成一个新的数列{cn},按从小到大的顺序排列为:1,4,16,25,….即为12,22,42,52,72,82,102,112,132,142,….即可得出.
解答 解:由an=3n-2,可得数列{an}的项由小到大排列为:1,4,7,10,13,16,…;
bn=n2,可得{bn}中所有的项按从小到大的顺序排列为:1,4,16,25,….
现抽出数列{an}、{bn}中所有相同的项并按从小到大的顺序排列成一个新的数列{cn},按从小到大的顺序排列为:1,4,16,25,….
即为12,22,42,52,72,82,102,112,132,142,….
则c10=142=196.
故答案为:196.
点评 本题考查了球两个数列相同的项的方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
6.若函数f(x)=log${\;}_{\frac{1}{2}}$(-x2+4x+5)在区间(3m-2,m+2)内单调递增,则实数m的取值为( )
| A. | [$\frac{4}{3},3$] | B. | [$\frac{4}{3},2$] | C. | [$\frac{4}{3},2$) | D. | [$\frac{4}{3},+∞$) |
3.某几何体的三视图如图所示,则该几何体的体积为( )
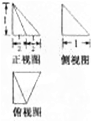

| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
20.某校组织一次校外活动,有10名同学参加,其中有6名男生,4名女生,从中随机抽取3名,其中至多有1名女生的概率( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
