题目内容
5.设a=(x2+y2)(x-y),b=(x2-y2)(x+y),若x<y<0,则a与b的大小关系为a>b.分析 把a与b作差,由差式大于0、等于0和小于0求解x的值或取值范围,由此得到a,b的大小关系.
解答 解:a-b=(x2+y2)(x-y)-(x2-y2)(x+y)=(x-y)[(x2+y2)-(x+y)2]=-2xy(x-y),
∵x<y<0,
∴x-y<0,xy>0,
∴a-b=-2xy(x-y)>0,
∴a>b,
故答案为:a>b.
点评 本题考查了不等式的大小比较,考查了作差法,训练了不等式的解法,是基础题.

练习册系列答案
相关题目
16.若f(x)=sin(2x+φ)为偶函数,则φ值可能是( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | π |
10.已知条件p:x>1或x<-3,条件q:5x-6>x2,则¬p是¬q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
14.某几何体的三视图如图所示,该几何体的体积为( )
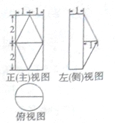

| A. | $\frac{16}{3}$ | B. | 5+$\frac{π}{3}$ | C. | $\frac{7π}{3}$ | D. | $\frac{8π}{3}$ |