题目内容
10．有四个游戏盘，将它们水平放稳后，在上面扔一颗小玻璃球，若小球落在阴影部分，则可中奖，要想中奖机会最大，应选择的游戏盘是（ ）| A． |  | B． |  | C． |  | D． |  |
分析 先明确是几何概型中的面积类型，分别求三角形与扇形的面积，然后求比值即可．
解答 解：（1）游戏盘的中奖概率为 $\frac{3}{8}$，
（2）游戏盘的中奖概率为$\frac{1}{4}$，
（3）游戏盘的中奖概率为$\frac{2}{6}$=$\frac{1}{3}$，
（4）游戏盘的中奖概率为$\frac{1}{3}$，
（1）游戏盘的中奖概率最大．
故选：A．
点评 本题主要考查几何概型中的面积类型，基本方法是：分别求得构成事件A的区域面积和试验的全部结果所构成的区域面积，两者求比值，即为概率．
练习册系列答案
活力试卷系列答案
课课优能力培优100分系列答案
相关题目
20．若sinα=$\frac{3}{5}$，且α是第二象限角，则tanα=（ ）
| A． | -$\frac{3}{4}$ | B． | $\frac{4}{3}$ | C． | $±\frac{4}{3}$ | D． | $±\frac{3}{4}$ |
2．已知角α的终边上一点P（-3，4），则cosα的值为（ ）
| A． | $\frac{4}{5}$ | B． | $\frac{3}{5}$ | C． | $-\frac{4}{5}$ | D． | $-\frac{3}{5}$ |
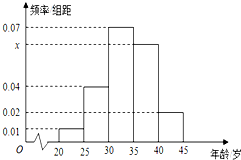为增强市民的节能环保意识，某市面向全市征召义务宣传志愿者．从符合条件的500名志愿者中随机抽取100名志愿者，其年龄频率分布直方图如图所示，其中年龄分组区间是：[20，25），[25，30），[30，35），[35，40），[40，45]．