Question

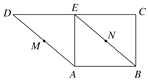
【题目】一个正方体的平面展开图及该正方体的直观图的示意图如图所示.

(1)请按字母F、G、H标记在正方体相应地顶点处(不需要说明理由)；

(2)判断平面BEG与平面ACH的位置关系．并说明你的结论；

(3)证明：直线DF⊥平面BEG.

Answer 1

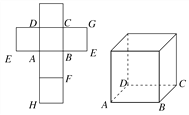
【答案】（1）见解析；（2）平面BEG∥平面ACH；（3）证明见解析

【解析】试题分析：(1)折叠成正方体即可得出；（2）根据条件可证四边形BCEH为平行四边形，因此BE∥CH，由线面平行判定定理即可得证；（3）根据DH⊥平面EFGH可得DH⊥EG，又EG⊥FH，可证EG⊥平面BFHD，所以DF⊥EG，同理可证同理DF⊥BG，所以命题得证．

试题解析：

　(1)点F、G、H的位置如图所示．

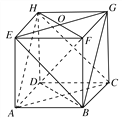
(2)平面BEC∥平面ACH．证明如下：

因为ABCD－EFGH为正方体，所以BC∥FG，BC＝FG，

又FG∥EH，FG＝EH，所以BC∥EH，BC＝EH，

于是四边形BCEH为平行四边形，

所以BE∥CH，

又CH平面ACH，BE平面ACH，

所以BE∥平面ACH，

同理，BG∥平面ACH，

又BE∩BG＝B，

所以平面BEG∥平面ACH．

(3)连接FH交EG于点O，连接BD．

因为ABCD－EFGH为正方体，所以DH⊥平面EFGH，

因为EG平面EFGH，所以DH⊥EG，

又EG⊥FH，EG∩FH＝O，

所以EG⊥平面BFHD，

又DF平面BFHD，所以DF⊥EG，

同理DF⊥BG，

又EG∩BG＝G，

所以DF⊥平面BEG．