题目内容
【题目】设A(n)表示正整数n的个位数,an=A(n2)﹣A(n),A为数列{an}的前202项和,函数f(x)=ex﹣e+1,若函数g(x)满足f[g(x)﹣ ![]() ]=1,且bn=g(n)(n∈N*),则数列{bn}的前n项和为 .
]=1,且bn=g(n)(n∈N*),则数列{bn}的前n项和为 .
【答案】n+3﹣(2n+3)?( ![]() )n
)n
【解析】解:n的个位数为1时有:an=A(n2)﹣A(n)=0,
n的个位数为2时有:an=A(n2)﹣A(n)=4﹣2=2,
n的个位数为3时有:an=A(n2)﹣A(n)=9﹣3=6,
n的个位数为4时有:an=A(n2)﹣A(n)=6﹣4=2,
n的个位数为5时有:an=A(n2)﹣A(n)=5﹣5=0,
n的个位数为6时有:an=A(n2)﹣A(n)=6﹣6=0,
n的个位数为7时有:an=A(n2)﹣A(n)=9﹣7=2,
n的个位数为8时有:an=A(n2)﹣A(n)=4﹣8=﹣4,
n的个位数为9时有:an=A(n2)﹣A(n)=1﹣9=﹣8,
n的个位数为0时有:an=A(n2)﹣A(n)=0﹣0=0,
每10个一循环,这10个数的和为:0,
202÷10=20余2,余下两个数为:a201=0,a202=2,
∴数列{an}的前202项和等于:a201+a202=0+2=2,
即有A=2.
函数函数f(x)=ex﹣e+1为R上的增函数,且f(1)=1,
f[g(x)﹣ ![]() ]=1=f(1),
]=1=f(1),
可得g(x)=1+ ![]() =1+
=1+ ![]() ,
,
则g(n)=1+(2n﹣1)( ![]() )n,
)n,
即有bn=g(n)=1+(2n﹣1)( ![]() )n,
)n,
则数列{bn}的前n项和为n+[1( ![]() )1+3(
)1+3( ![]() )2+5(
)2+5( ![]() )3++(2n﹣1)(
)3++(2n﹣1)( ![]() )n],
)n],
可令S=1( ![]() )1+3(
)1+3( ![]() )2+5(
)2+5( ![]() )3++(2n﹣1)(
)3++(2n﹣1)( ![]() )n,
)n,
![]() S=1(
S=1( ![]() )2+3(
)2+3( ![]() )3+5(
)3+5( ![]() )4++(2n﹣1)(
)4++(2n﹣1)( ![]() )n+1,
)n+1,
两式相减可得 ![]() S=
S= ![]() +2[(
+2[( ![]() )2+(
)2+( ![]() )3+(
)3+( ![]() )4++(
)4++( ![]() )n]﹣(2n﹣1)(
)n]﹣(2n﹣1)( ![]() )n+1
)n+1
= ![]() +2
+2 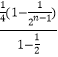 ﹣(2n﹣1)(
﹣(2n﹣1)( ![]() )n+1,
)n+1,
化简可得S=3﹣(2n+3)( ![]() )n,
)n,
则数列{bn}的前n项和为n+3﹣(2n+3)( ![]() )n.
)n.
故答案为:n+3﹣(2n+3)( ![]() )n.
)n.
先根据n的个位数的不同取值推导数列的周期,由周期可求得A=2,再由函数f(x)为R上的增函数,求得g(x)的解析式,即有bn=g(n)=1+(2n﹣1)( ![]() )n,再由数列的求和方法:分组求和和错位相减法,化简整理即可得到所求和.
)n,再由数列的求和方法:分组求和和错位相减法,化简整理即可得到所求和.