Question

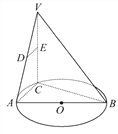
【题目】AB是☉O的直径，点C是☉O上的动点(点C不与A，B重合)，过动点C的直线VC垂直于☉O所在的平面，D，E分别是VA，VC的中点，则下列结论中正确的是________(填写正确结论的序号).

(1)直线DE∥平面ABC.

(2)直线DE⊥平面VBC.

(3)DE⊥VB.

(4)DE⊥AB.

Answer 1

【答案】(1)(2)(3)

【解析】因为AB是☉O的直径，点C是☉O上的动点(点C不与A，B重合)，所以AC⊥BC，

因为VC垂直于☉O所在的平面，所以AC⊥VC，又BC∩VC=C，所以AC⊥平面VBC.

因为D，E分别是VA，VC的中点，所以DE∥AC，又DE平面ABC，AC平面ABC，所以DE∥平面ABC，DE⊥平面VBC，DE⊥VB，DE与AB所成的角为∠BAC是锐角，故DE⊥AB不成立.由以上分析可知(1)(2)(3)正确,故填(1)(2)(3).